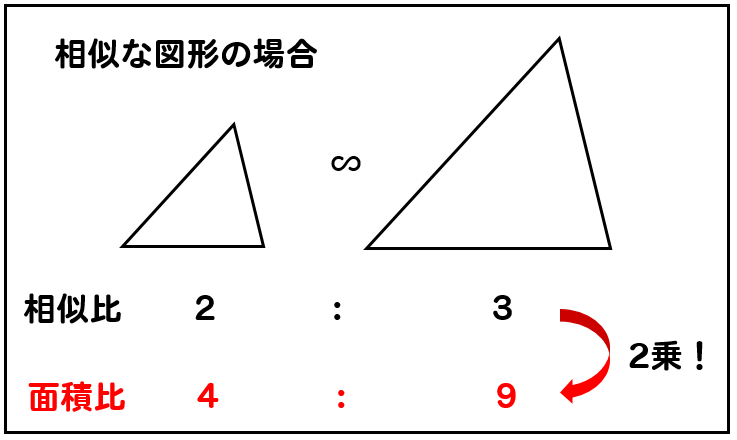
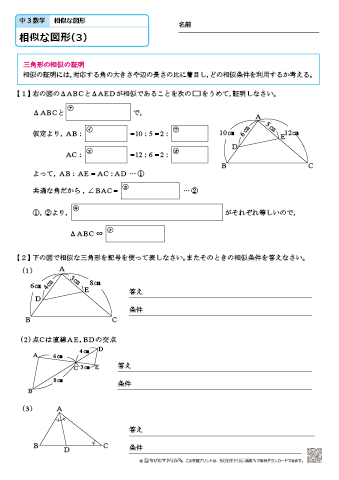
相似な図形には、次の \(2\) つの性質があります。 性質①対応する辺の長さの比はすべて等しい 相似な図形では、対応する辺の長さの比が等しくなります。 相似な図形では、対応するすべての線分が同じ倍率で拡大・縮小されています。 つまり、辺 \(a'\) が辺 \(a\) の \(2\) 倍の長さであ・相似な図形の性質について理解し,それを数学の用語や記号を用いて簡潔に表現した り,それを用いて線分の長さを求めたりすることができる。 ・平行線と線分の比についての性質を理解し,それを用いて線分の長さを求めたりする ことができる。 ・相似な図形の相似比と面積比及び体積~任意図形の作図から柔軟な思考で,相似な図形の性質を見いだす 数学科学習指導法の研究~ 1 単元名 「図形の相似」(全18時間) 2 本単元における基本的な考え ここで育てたい力とは, ここで育てたい力とは,抽象的な図形という教材のなかで,2つの図形間の関係を考 えることにより

令和3 21 年度用 中学校数学 内容解説資料a
数学 相似な図形の性質
数学 相似な図形の性質-相似な図形の性質を活用して,影の長さから校舎の 高さを求める方法を考える。 縮図をかいて,2地点間の距離を求めること 21 影の長さから校舎の高さを求めること 22 章末問題 6.本時の学習指導 (1) 本時の目標 ・根拠を明らかにし、相似を用いて説明できる。考え方 (2) 本時の評価・相似な図形の性質,三角形の相似条件などを,数学の用語や記号を用いて簡潔に表現するなど, 技能を身に付けている。 数量や図形などについての知識・理解 ・相似の意味,三角形の相似条件,平行線と線分の比についての性質,相似比と面積比及び体積比 の関係などを理解し,知識



Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Zissenmoderu Documents C 053 Pdf
①相似な図形の作図方法から相似な 図形の性質や相似比を見いださせ る。 ②相似な図形の性質や相似比の意味 を理解させる。 中学校を上空から撮影した 写真を見て,それぞれの建物 の大きさを考える。 相似な図形の作図方法を考 える。相似な図形の性質を用いて考察することができるようにする。 (1)平面図形の相似の意味及び三角形の相似条件について理解することができるようにする。 (2)三角形の相似条件などを基にして図形の基本的な性質を論理的に確かめることができる ようにする。 (3)平行線と線分の比に 三角形の角の二等分線の性質の証明がわかる5ステップ ゆうき先生 三角形の二等分線の定理の証明は、 補助線をひく 相似な図形をみつける 辺の比に注目する 二等辺三角形をさがす 証明をかく の5ステップだよ。
相似条件を用いた図形の性質の論証や,数学的な推論の意義と方法について理解を深める。 B 主として「活用」に関する問題 4(1)(2) (1)問題の概要 図形についての証明を読み,証明を振り返って評価することやその評価に基づいて証明を改善す る問題である。 (2)出題の趣旨 証明に・ 相似な図形の性質を活用した問題解決(4 時間) 6 本時の指導 本時の目標 ・ 証明を見直して,その根拠に合同を用いている場合に,相似に置き換えられないか考えるという考 え方を理解する。 本時の教材について 621 本時で扱う題材について 本時で扱う題材は以下の図形の性質である相似な図形の性質を用いて、拡大図・縮図をかいたり、線分の長さや面積、体積を求めたりすることができる。 数学的な技能 平面図形の相似の意味及び三角形の相似条件,基本的な立体の相似の意味と相似な図形の相似比と面積比及び体 積比の関係について理解している。 数量や図形
3.相似な図形の性質を理解 し、相似比や対応する辺の長さ を求める。 2つの図形が 相似であるこ とから、相似 比や対応する 辺の長さを求 めることがで きる。(練習問 題の解決状況 の分析) 相似比を理解 している。(練 習問題の解決 状況の分析) 4 1.三角形の相似条件について 理解相似な図形の性質 相似な図形では対応する線分(辺の長さ)の比がみな等しい。 相似な図形では対応する角の大きさがそれぞれ等しい。 前のページ 次のページ相似な図形の性質を用いて考察することができる。 (2) 観察、操作や実験などの活動を通して、円周角と中心角の関係を見いだして理解し、それを用 いて考察することができるようにする。 (3) 観察、操作や実験などの活動を通して、三平方の定理を見いだして理解し、それを用いて考察




中3数学 拡大図 縮図の作図 映像授業のtry It トライイット
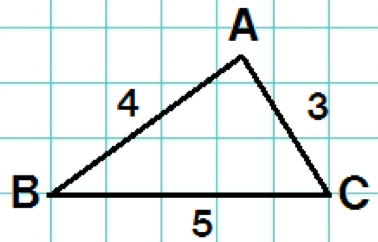



中3数学 覚えて損はない 相似な図形の性質2つ Qikeru 学びを楽しくわかりやすく
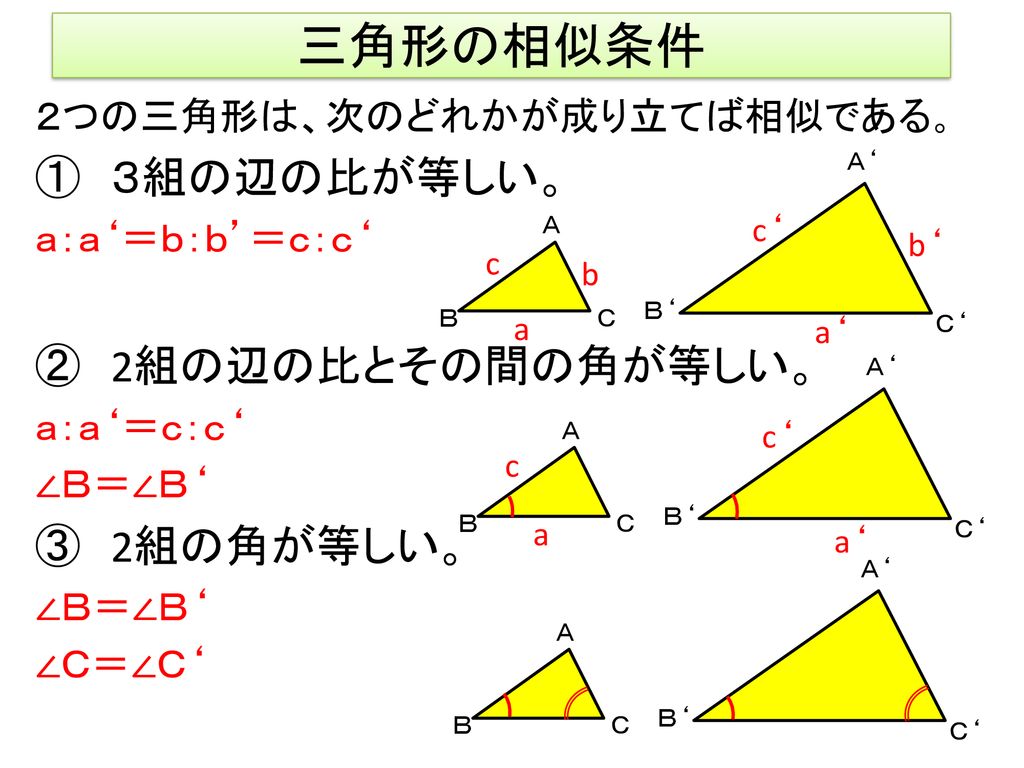
・ 相似の概念を明らかにし、2つの相似な図形を観察して、相似な図形の性質を考えること ができる。 ・ 相似の意味、性質、相似比について理解する。①相似な図形の性質 を理解している。 ②三角形の相似条件 を理解している。 ③相似の考えを用い た間接的な高さや 距離の求め方を理 解している。 ④中点連結定理を理 解している。 ⑤平行線と比の性質 を理解している。 ⑥相似な図形の相似 比と面積比の関係 を理解している。 ⑦相似な相似図形の性質 相似図形については,3組の辺の比が等しくなる. ⇒ この公式を使って辺の長さを求めることができる. 図1例 右図1で ab//cd のとき, aeb と dec が相似図形になる (証明) aeb と dec について ∠ aeb= ∠ dec (対頂角は等しい) ∠ abe= ∠ dce (平行線の錯角は等しい




令和3 21 年度用 中学校数学 内容解説資料a




中3数学 覚えて損はない 相似な図形の性質2つ Qikeru 学びを楽しくわかりやすく
相似な図形の性質を使って、線分の長さを求めよう。 辺の長さや角の大きさを求 ・向きが変わるとわかりにくい人は、向きをそろえた図を自分でかめることができる。 いてから、考えると良い。 (数学的な技能) 三角形の合同条件を基にし 三角形の相似条件について考えよう て、三角形のな立体の相似の意味を理解し,相似な図形の性質を用いて図形の計量ができるようにすることがね らいとなる。 「b 図形」においての系統 中学校3年 2 生徒観 今年度4月19日(火)に実施した全国学力学習状況調査において図形領域における,平均正答率 は,数学a 661(全国差―10),数学b 2(全国相似な図形の性質の活用 ・ 相似の問題を解く4ポイント 1 「実数値」と「比」をきちんと区別する 2 山型・蝶型を発見する 3 「補助線」を引いて、「山型」「蝶型」をつくる 4




中3数学 相似 台形の対角線 Youtube



1
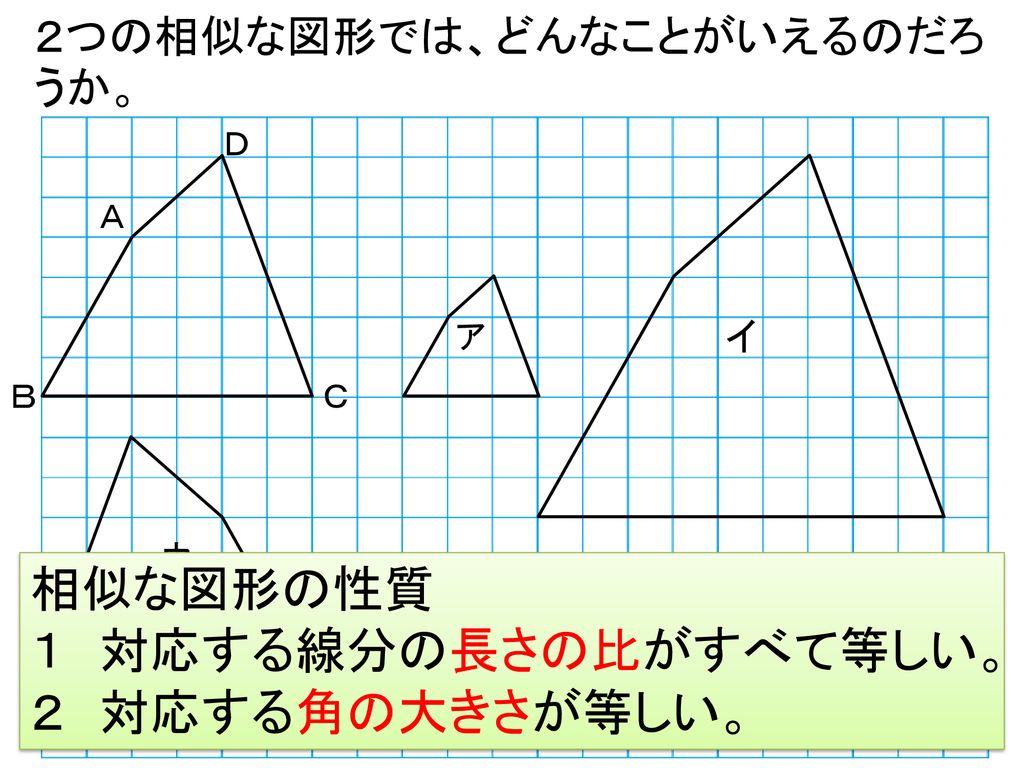
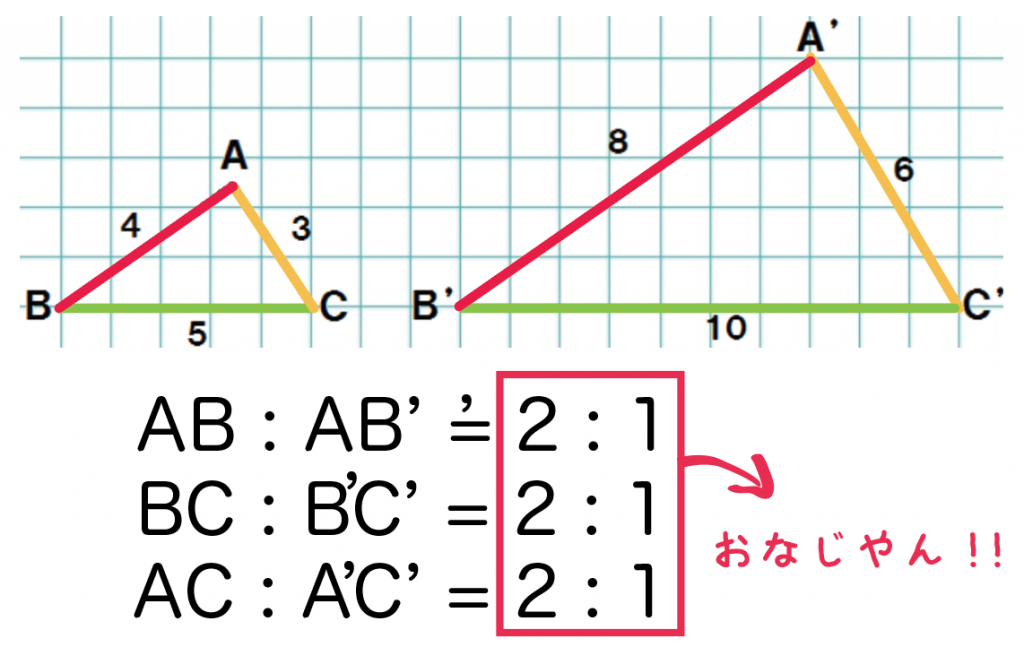
『相似な図形』の単元の中から 平行線と線分の比という内容について解説してきます。 ここでは、相似な図形の性質をつかって いろんな図形の辺の長さを求めていきます。 長々と解説をするよりも 問題を見ながら、実践を通して学習するのが良いので相似な図形 相似な図形の性質2(2) 無料で使える中学学習プリント cm cm cm cm B CE F cm cm 次の①〜⑥で、2つの図形が常に相似であるものを記号で答えなさい。 ①2つの長方形 ②2つの正三角形 ③2つの正方形 ④2つのひし形 ⑤2つの直角二等辺三角形 ⑥2つの直角三角形 下の DEFは ABCを縮小し相似を定義している.そして,帰納的推論により, 相似な図形の性質 1 対応する線分の比はすべて等しい 2 対応する角はそれぞれ等しい を導いている2 多角形に対しては,相似な図形の性質は相似であることの必要十分条件になっている.




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



第5章4 三角形の相似 相似な図形の性質 2 ニュージーランド短期留学ダイアリー
性質を理解し,相似な図形 図形の拡大図をかく。 大図をかこうとしている。 をかいたり,相似比や辺の 2 長さを求めたりすることが ・相似な関係や辺,角の大きさの関 図形の相似の意味と表し方,及び相似な図形の性質を できる。 係を調べ,関係を数学A /図形の性質「平面図形」 5 / ??・相似な図形の性質や相似の意味及び対応する頂点,辺,角について理解 するとともに,2つの図形が相似であることを記号∽を使って表すこと 知 知:ノート 知識・技能 思考・判断・表現 主体的に学習に取り組む態度 ・平面図形の相似の意味及び三角 形の相似条件について理解して いる




中学3年生 数学 大日本図書 相似な図形 三角形と比の定理 教科書練習問題 赤城 ᐡᐤᐡ
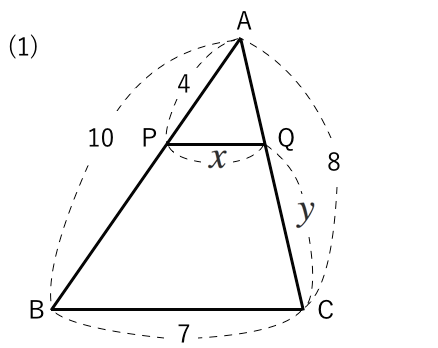



相似な図形 長さを求める 苦手な数学を簡単に
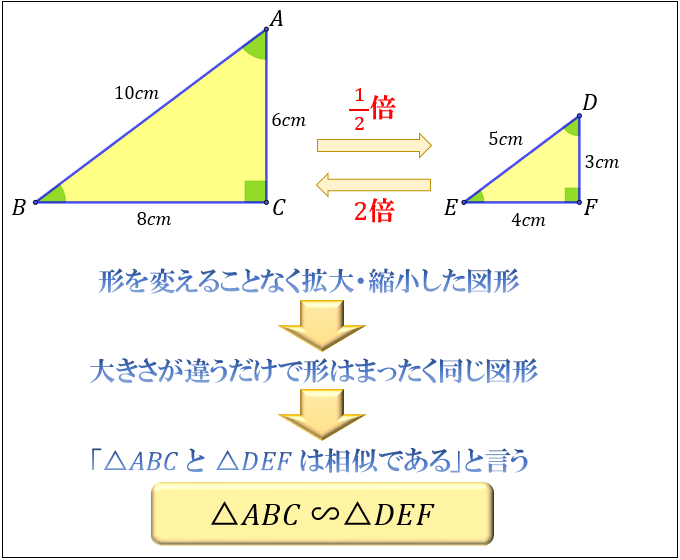
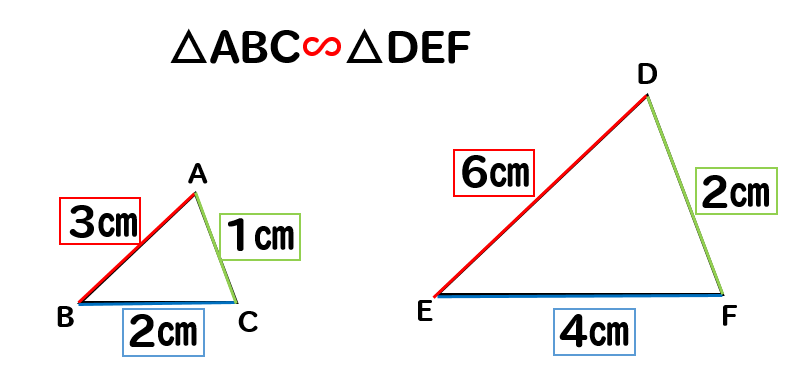
「同じ形のまま拡大・縮小した図形である」ことを、 相似 と言います。 たとえば、下図の三角形 D E F は「三角形 A B C の形を変えることなく 1 2 倍に縮小した図形」です。本頁面最後修訂於21年4月28日 (星期三) 0818。 本站的全部文字在創用CC 姓名標示相同方式分享 30協議 之條款下提供,附加條款亦可能應用。 (請參閱使用條款) Wikipedia®和維基百科標誌是維基媒體基金會的註冊商標;維基™是維基媒體基金會的商標。 維基媒體基金會是按美國國內稅收法501(c)(3相似な図形の性質 一般に、相似な図形では、次のことが成り立つ。 対応する線分の長さの比はすべて等しい。 対応する角の大きさはそれぞれ等しい。 また、円は半径に関わらず常に同じ形をしているので、すべて相似な図形であるといえます。 また、2




相似な図形に慣れる あかつき指導会のブログ
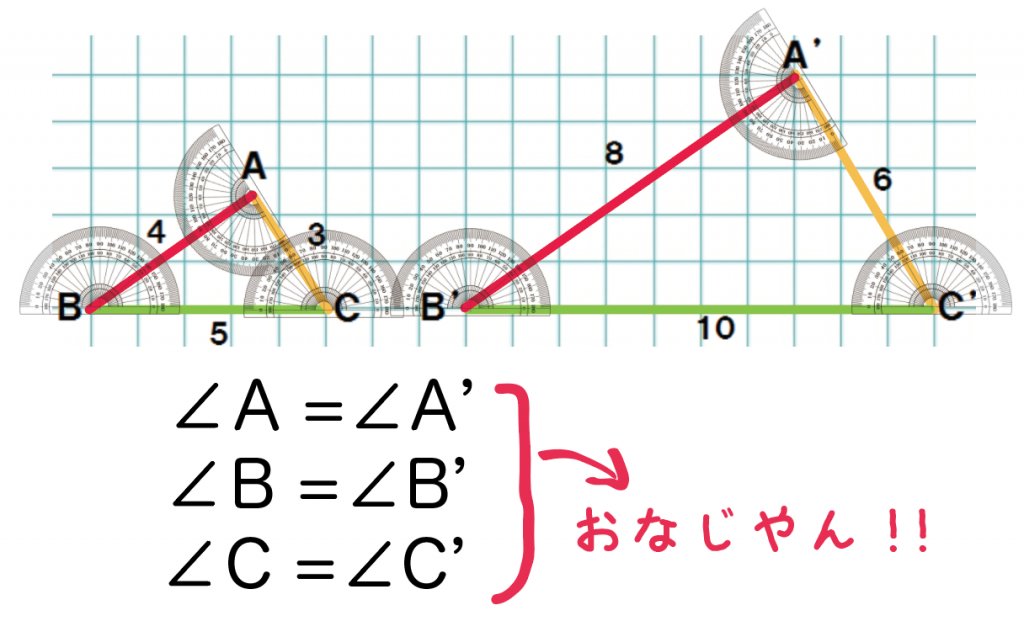



中3数学 覚えて損はない 相似な図形の性質2つ Qikeru 学びを楽しくわかりやすく
中点でなかったとしても、中点連結定理の性質は成立します。 相似の図形では、各辺の相似比はすべて同じです。今回の場合、 ABC∽ AMNの相似比は3:1です。そのため、 一つの辺の長さが分かれば他の辺の長さについても計算できるようになります。 例えば、MNの長さが3cmの場合、MN:BC=1:3の<相似な図形の性質> 相似な図形では,対応する部分の長さの比はすべて等しく,対応する角の大きさはそれ ぞれ等しい。 ・言葉の抽象度が高く,何をいっているか分からない。 言い換えをしたり,単文にしたりする。 一定の割合に拡大 「(図を指しながら)ここはここの2倍 だね。ここも相似な図形の性質,三 角形の相似条件など を,数学の用語や記号 を用いて簡潔に表現す る技能を身に付けてい る。 相似の意味,三角形の 相似条件,平行線と線 分の比についての性 質,相似比と面積比及 び体積比の関係を理解 し,知識を身に付けて いる。 4 単元について (1) 教材観 小学校



2



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典
相似な図形の性質 名前 右の図で a d 四角形abcdと四角形efghが ° e h 相似であるとき、 cm 次の問いに答えなさい。 ①辺abの長さを求めなさい。 b cm c f cm g ②∠eの大きさを求めなさい。 右の図で abcと def が相似であるとき 次の問いに答えなさい。か 相似な図形の性質を知る。 相似な図形のかき方や にして取り組むよう助言する。 進んで相似な図形やその む 性質に興味をもち、自 性質について調べてい ( 北海道の形を3倍にする作図をし 分で拡大・縮小の意味 ・発見したことを、まずは自分の言葉で表現すれば る。 T や相似な図形のて,相似な図形の性質を用 いることで,図形の性質な どを考えることができる。 ⑧ 図形の辺の比の関係を求 めたり,直接測定できない 高さや距離などを縮図をか いて求めたりすることがで きる。 ⑤ 日常生活で相似な図形の性 質を利用している場面を理解 している。 (2) 単元の指導と評価
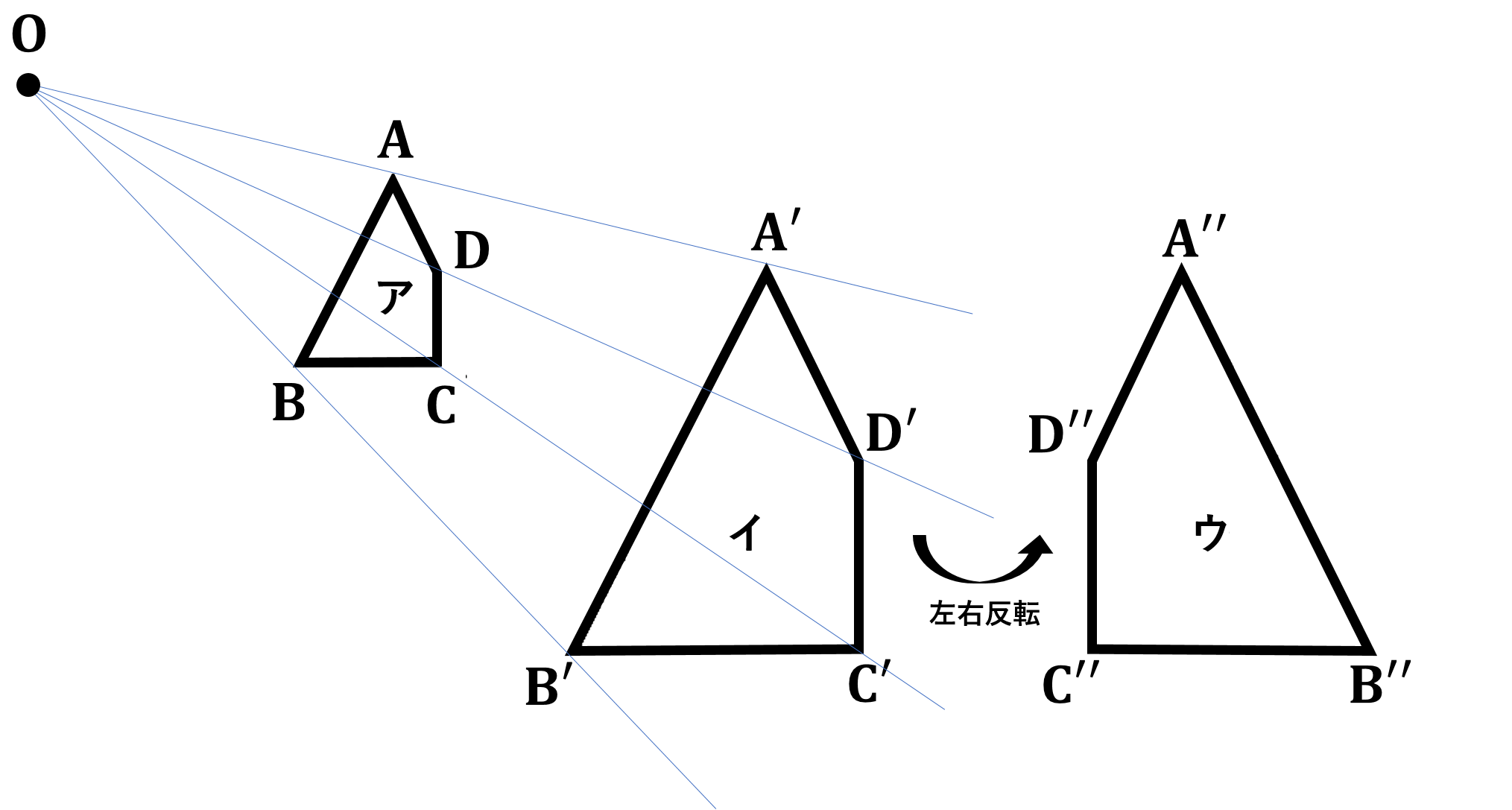



5章 相似 タカラゼミ




相似な図形の性質 中3数学 図形と相似1 Youtube
相似を表す記号 4ABC と4DEF が そうじ 相似のとき 4ABC ˝ 4DEF と表す. 三角形の相似条件 a b c ka kb kc a b ka kb 三角形が相似になる条件は次である. 1 3 辺の辺の比がすべて等しい ˆ 相似比1 k 2 2 辺の辺の比とその間の角がそれぞれ等しい ˆ 相似比1 k・相似な図形の性質について学んだことを生活や学習に生かそうとしている。 態② ・相似な図形の性質を具体的な場面で活用することができる。思③ (3) 本時の展開 指導と学習活動 評価と配慮事項 1 前時までの振り返りをする。 いくつか紹介する 相似な図形の角の大きさや辺の長さ(3)相似な図形の性質を用いて、拡大図や縮図をかいたり、線分の長さや図形の面積、体積 を求めたりすることができる。 (数学的な技能) (4)相似な図形の意味や性質について説明することができる。 (数量や図形などについての知識・理解) 3.指導にあたって (1)生徒観 これまでの学習の




本時のねらい 相似の意味と性質を理解し 相似な図形の辺の長さや角度を求めることができる Ppt Download




相似な図形の性質 無料で使える中学学習プリント



相似とは何か その意味 合同との違い 相似な図形が持つ性質について アタリマエ



本時のねらい 図形の中から相似な三角形を見出し 相似条件を用いて証明することができる Ppt Download




相似な図形の性質 無料で使える中学学習プリント




相似な図形の性質 無料で使える中学学習プリント



この2と3の答え 何か分かりますか 中3の相似の図形です Yahoo 知恵袋
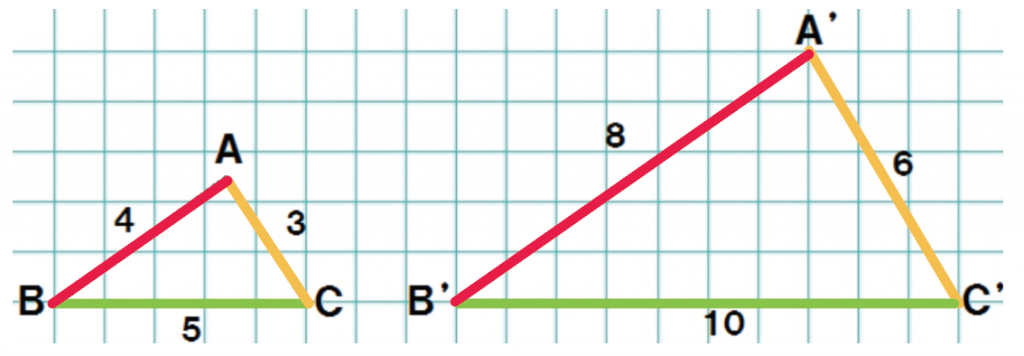



中3数学 覚えて損はない 相似な図形の性質2つ Qikeru 学びを楽しくわかりやすく



三角形の相似条件の解説 図形の性質



中学数学 図形の相似




本時の目標 身近にある事象を 相似な図形の性質を使って解決することができる Ppt Download



相似 平行四辺形と面積比の問題を徹底解説 数スタ



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




相似を使って何をしているのかがわかりません Clear




中3 数学 相似な図形 授業ノート 中学生 数学のノート Clear



本時のねらい 相似の意味と性質を理解し 相似な図形の辺の長さや角度を求めることができる Ppt Download



中3数学 線分の比と相似比の定期テスト過去問分析問題 Atstudier



中3数学 相似の基本性質をわかりやすく問題解説 数スタ



2



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中3数学 相似な図形の表面積比 体積比 映像授業のtry It トライイット



2



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典



中3数学 覚えて損はない 相似な図形の性質2つ Qikeru 学びを楽しくわかりやすく




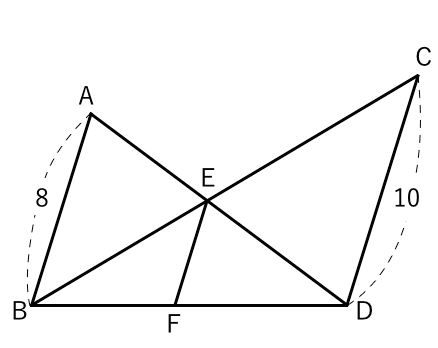
B Bar8cm C E Bar10cm G Lihat Cara Penyelesaian Di Qanda



Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Zissenmoderu Documents C 047 Pdf




中3数学 覚えて損はない 相似な図形の性質2つ Qikeru 学びを楽しくわかりやすく
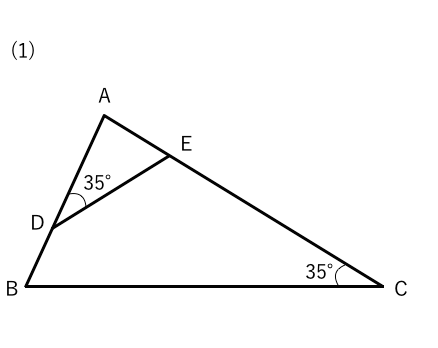



相似な図形 相似条件の練習問題 苦手な数学を簡単に




数学 相似の定理まとめ 中学生 数学のノート Clear



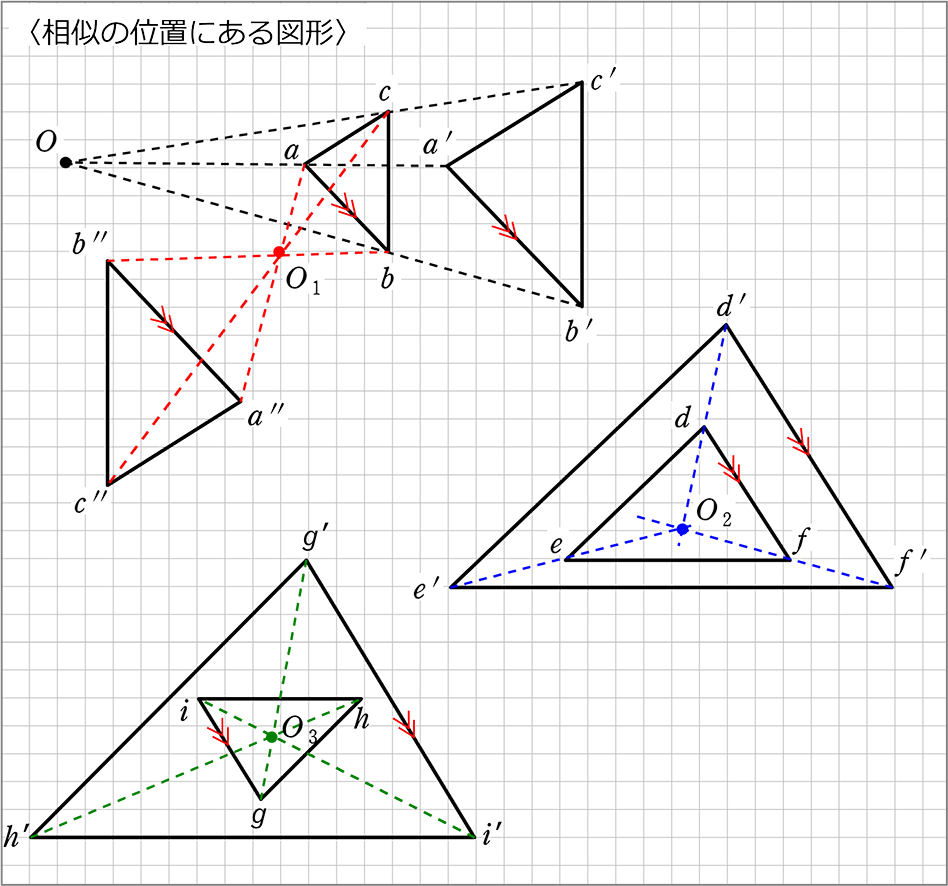
相似の位置 相似の中心とはなんですか 2つの図形の対応す Yahoo 知恵袋
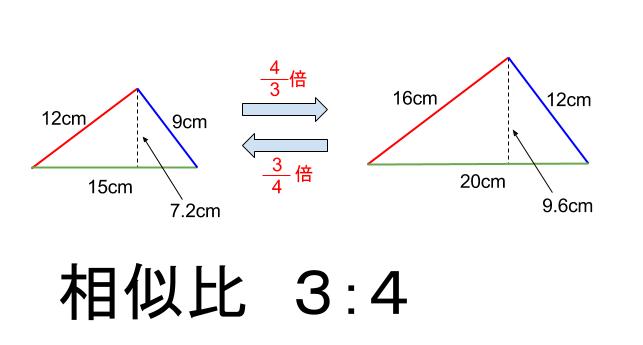



中学数学 相似とは何か 導入 中学数学の無料オンライン学習サイトchu Su



相似の中心と作図 Youtube
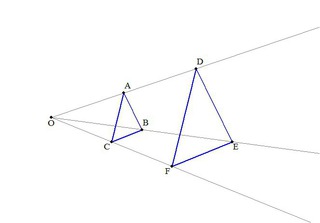



中学校数学 3年生 図形 相似な図形 Wikibooks



高校入試 英語 数学 図形と相似 相似の基礎
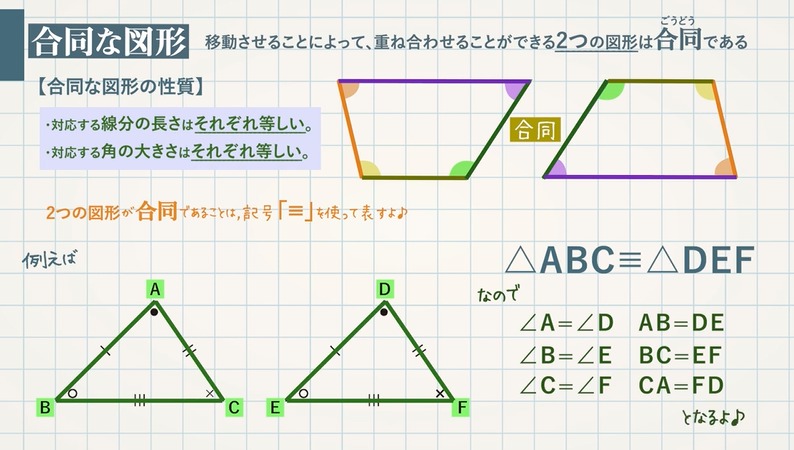



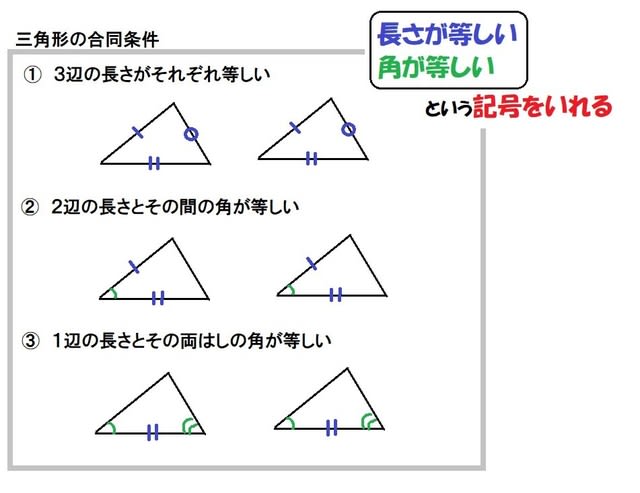
合同な図形とは 三角形の合同条件 教遊者



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典




中3数学 覚えて損はない 相似な図形の性質2つ Qikeru 学びを楽しくわかりやすく




相似な図形 計算 台形 練習問題 苦手な数学を簡単に




相似な図形や中心の作図 中3数学 Youtube




3数 相似な図形の性質と相似比 Youtube
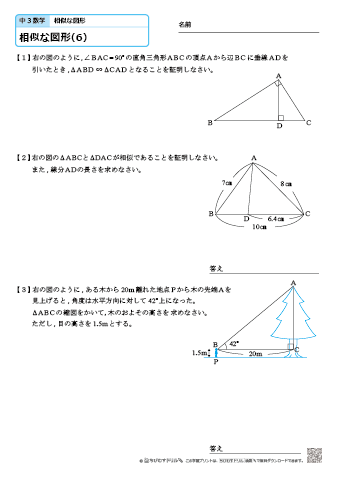



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
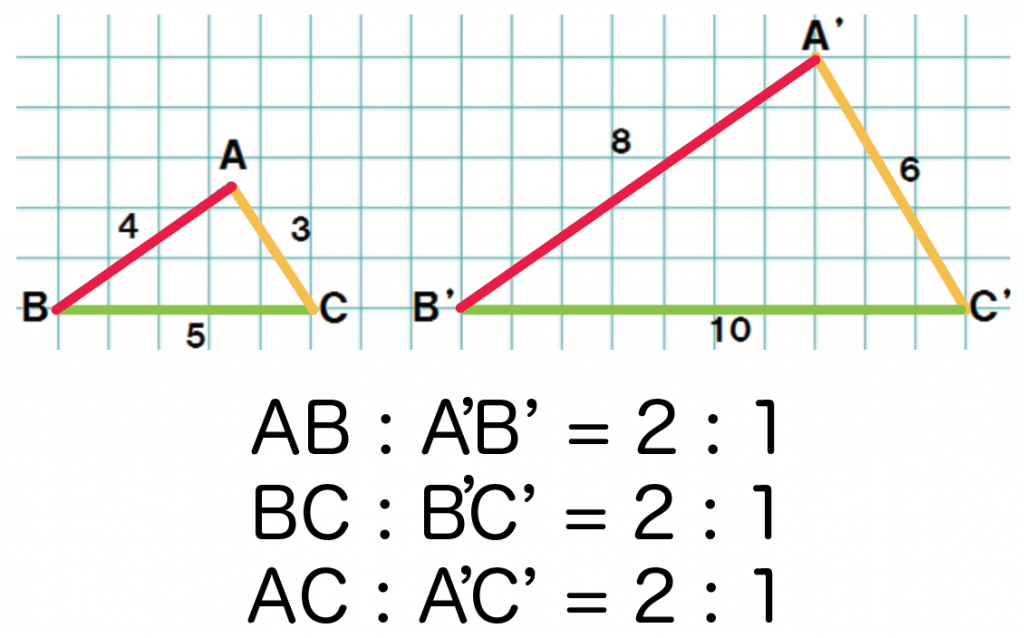



中3数学 覚えて損はない 相似な図形の性質2つ Qikeru 学びを楽しくわかりやすく
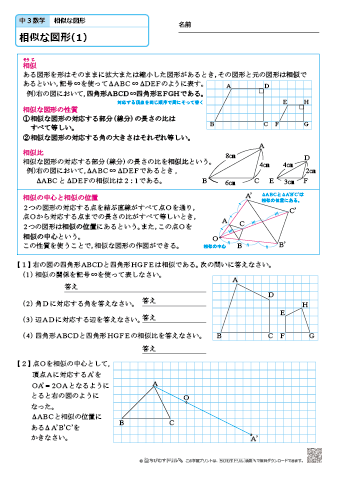



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



Ir Lib Shimane U Ac Jp




簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく




中3数学 覚えて損はない 相似な図形の性質2つ Qikeru 学びを楽しくわかりやすく



3年 相似な図形とその性質 数学イメージ動画集 大日本図書



1




中3数学 相似な図形の見つけ方 相似条件とは 基本問題を使って解説 数スタ




相似な図形の面積と体積 の勉強法のわからないを5分で解決 映像授業のtry It トライイット



合同な図形 小5 合同条件は超重要 算数の教え方教えますmother S Math Happy Study Support



Studydoctor相似な図形や中心の作図 中3数学 Studydoctor
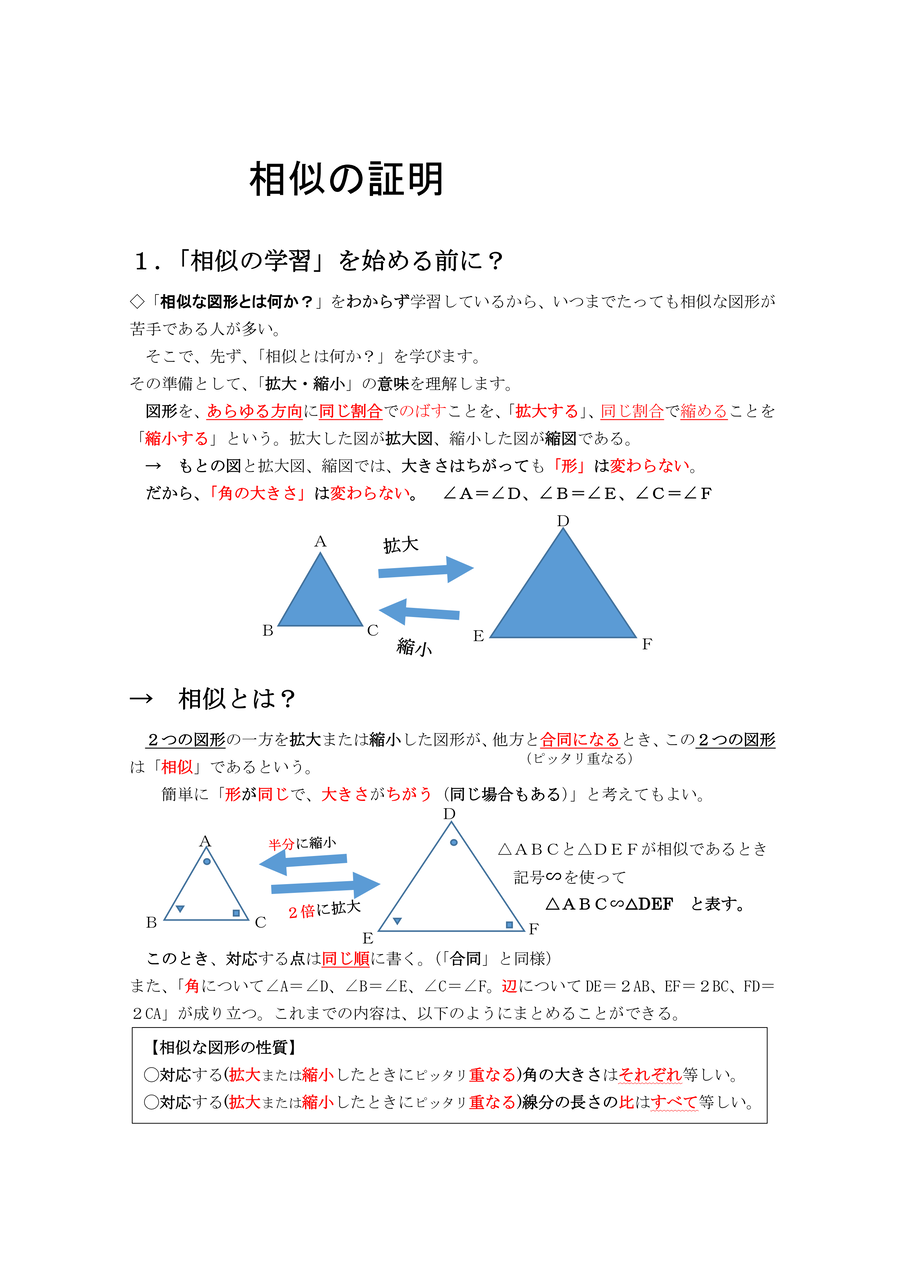



中学校数学 証明のコツ 相似




โน ตของ 中3 数学 相似な図形 ช น Junior High数学 Clear



Studydoctor相似な三角形の辺の比 中3数学 Studydoctor



相似な図形 ピンポイント計算式 苦手な数学を簡単に



相似の例題解説 01 相似な図形 操作 目次の項目 をクリックすると 解答画面に行きます Rei1 Jpg 解答画面 拡大縮小の図形シミュレーター Rei011 Jpg 02 相似な図形のかき方 Rei2 Jpg 03 相似な図形のかき方 Rei3 Jpg 04 相似な図形の



1




世界一わかりやすい数学問題集中3 5章 図形と相似
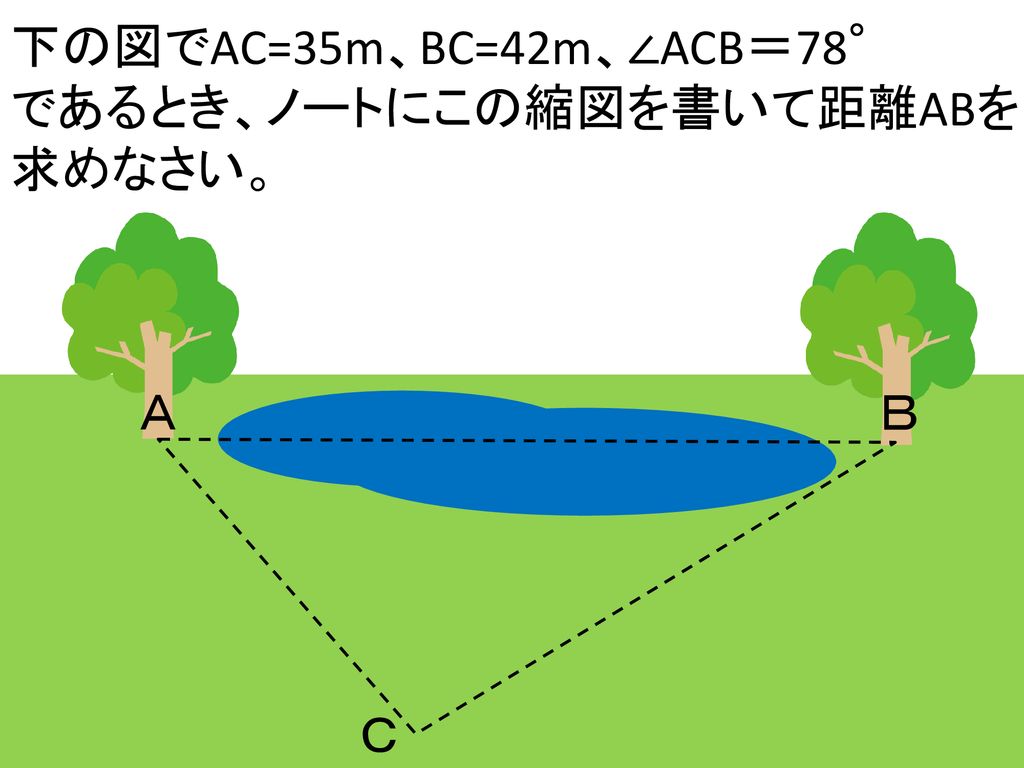



本時の目標 身近にある事象を 相似な図形の性質を使って解決することができる Ppt Download



Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Zissenmoderu Documents C 053 Pdf
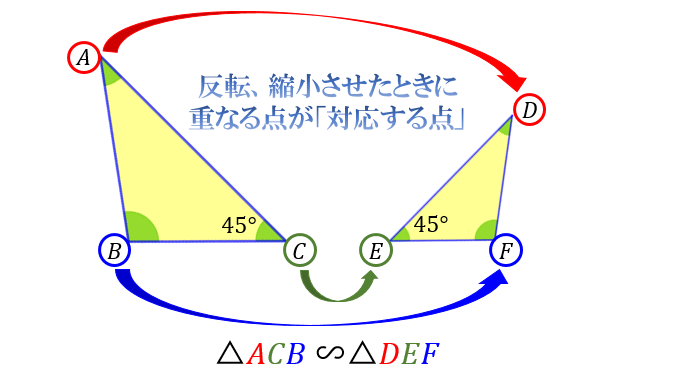



相似とは何か その意味 合同との違い 相似な図形が持つ性質について アタリマエ



Studydoctor図形の性質と相似の証明 中3数学 Studydoctor




3年 相似な図形とその性質 数学イメージ動画集 大日本図書



5 1 相似な図形の性質 ホンわか先生
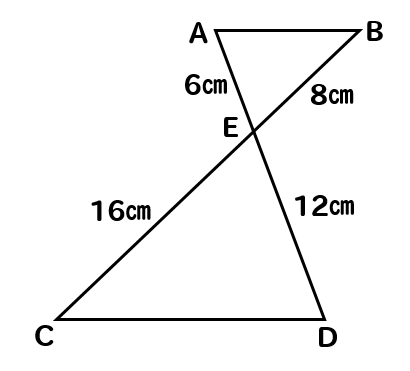



中3数学 相似な図形の見つけ方 相似条件とは 基本問題を使って解説 数スタ




中3数学 図形と相似9 相似条件と証明 折り返しの図形 すべて無料 星組の中学数学講座
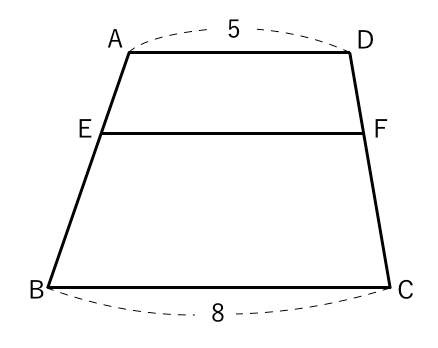



相似な図形 計算 台形 練習問題 苦手な数学を簡単に



中3数学 相似の基本性質をわかりやすく問題解説 数スタ




中3数学 相似の基本性質をわかりやすく問題解説 数スタ




相似な図形 補助線を引いて考える相似の問題 中学生からの勉強質問 数学 進研ゼミ中学講座




相似 台形と面積比の問題を徹底解説 数スタ



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典



2
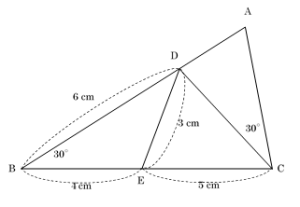



相似な図形 おやじさん ネット
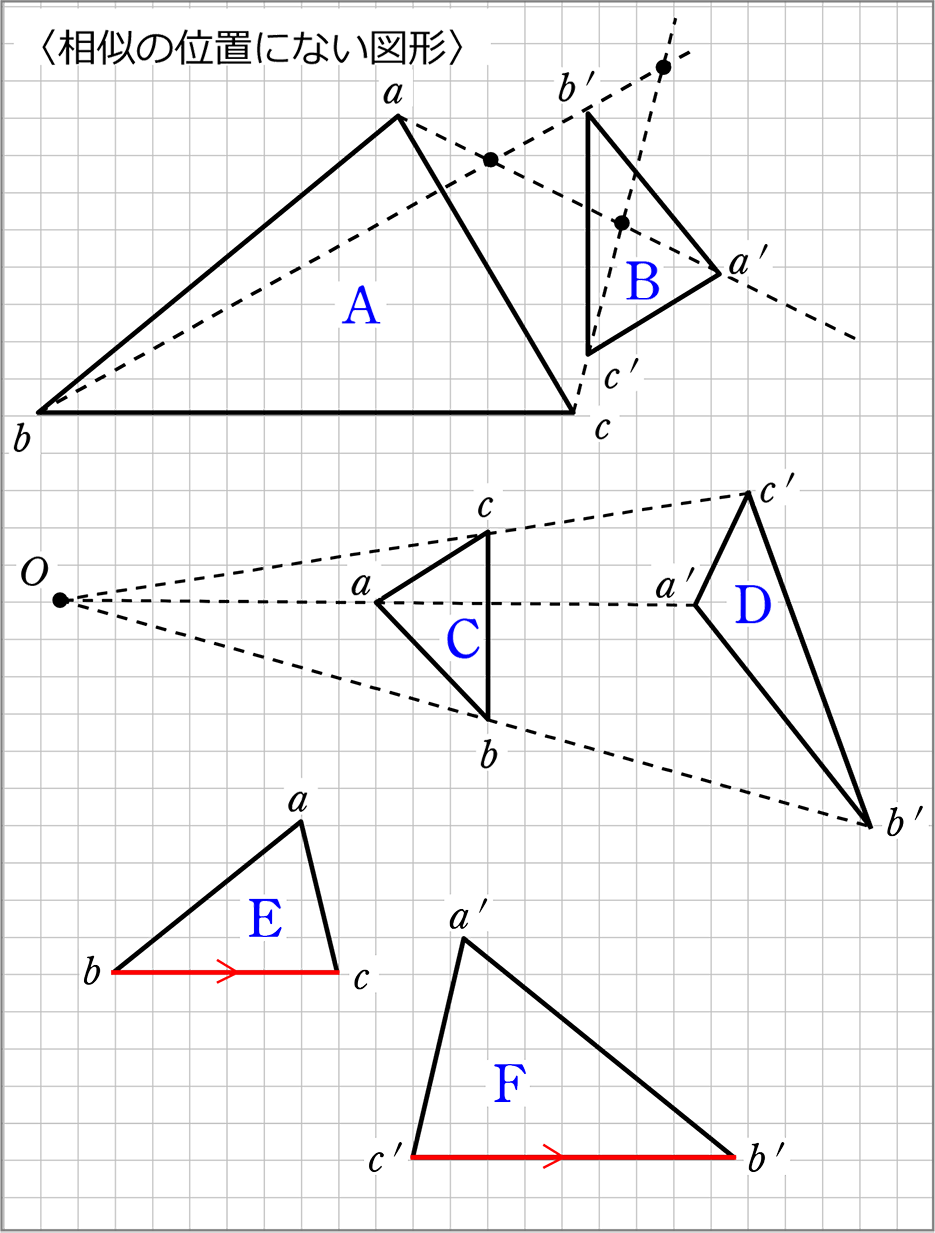



中学数学 図形の相似



1



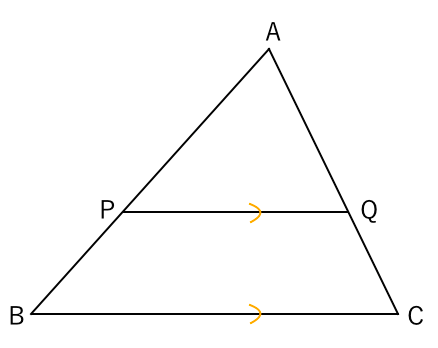
第5章3 三角形の相似 相似な図形の性質 中学生



相似な図形 計算 台形 練習問題 苦手な数学を簡単に
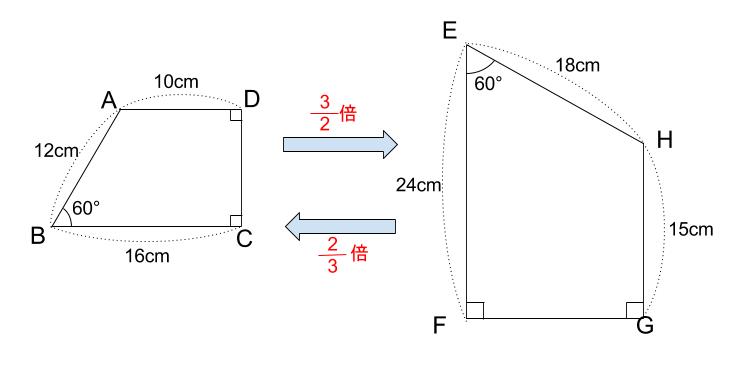



中学数学 相似とは何か 導入 中学数学の無料オンライン学習サイトchu Su




解き方を教えてください 答えは4分の9です Clear
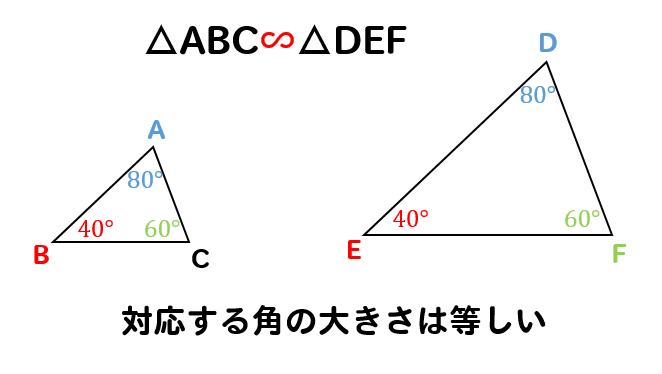



中3数学 相似の基本性質をわかりやすく問題解説 数スタ



Studydoctor相似の位置と中心 中3数学 Studydoctor




中3数学 拡大図 縮図の作図 練習編 映像授業のtry It トライイット
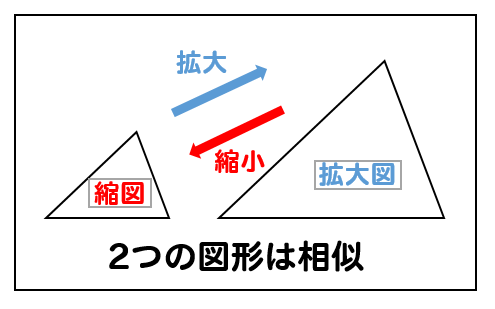



中3数学 相似の基本性質をわかりやすく問題解説 数スタ




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学
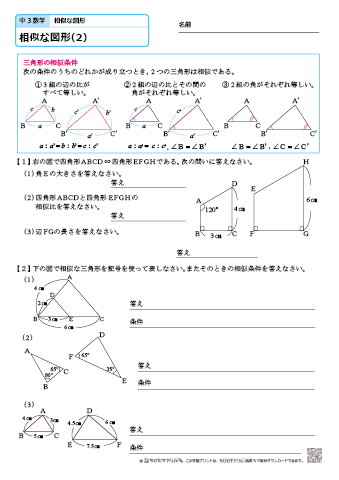



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
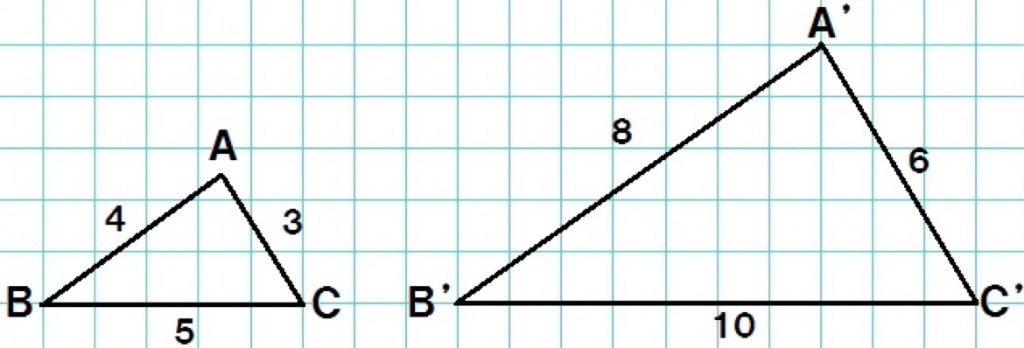



中3数学 覚えて損はない 相似な図形の性質2つ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿