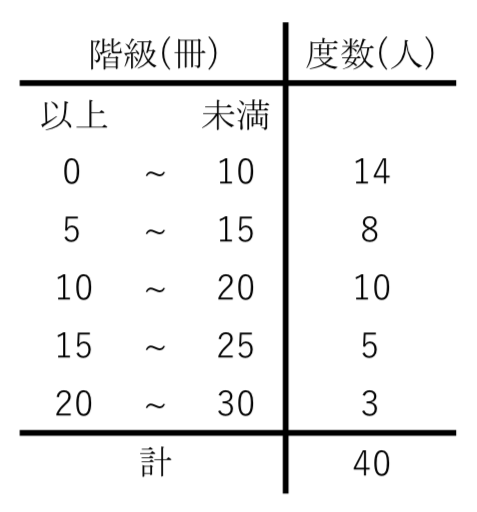
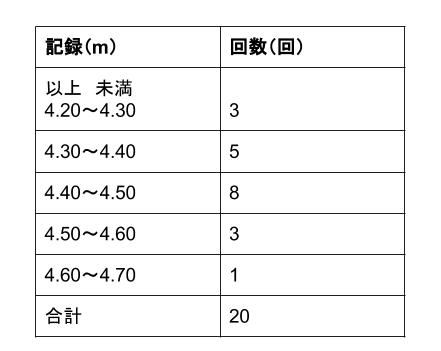
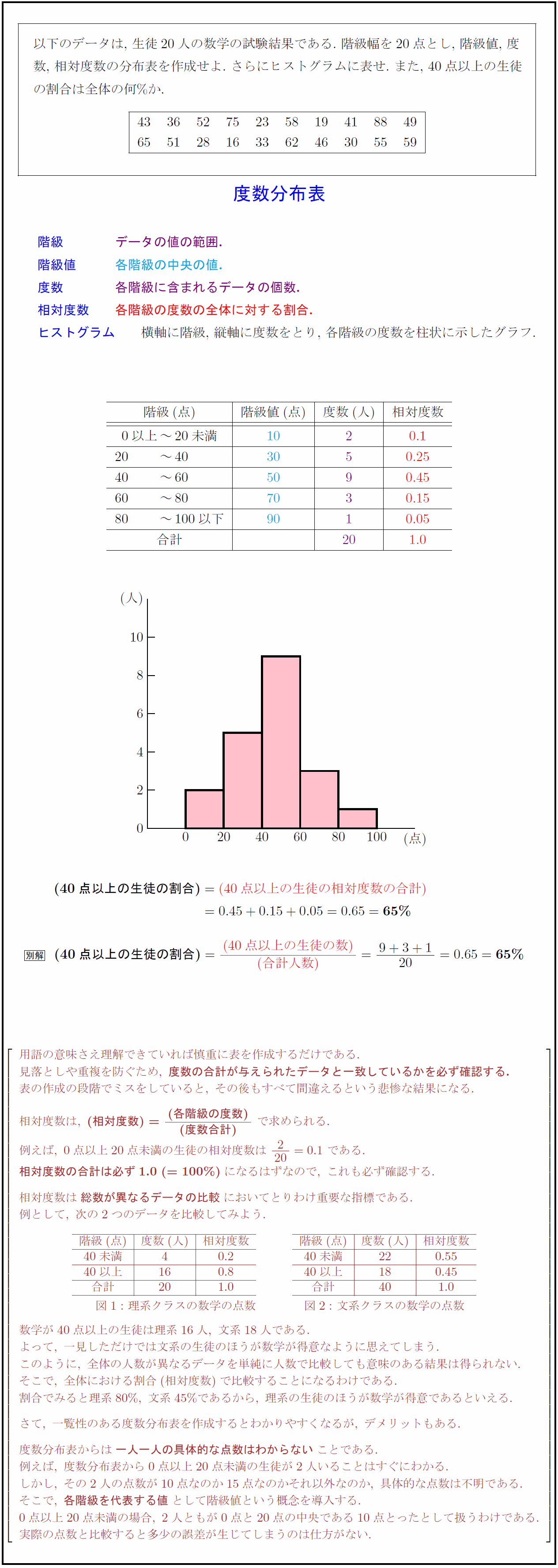
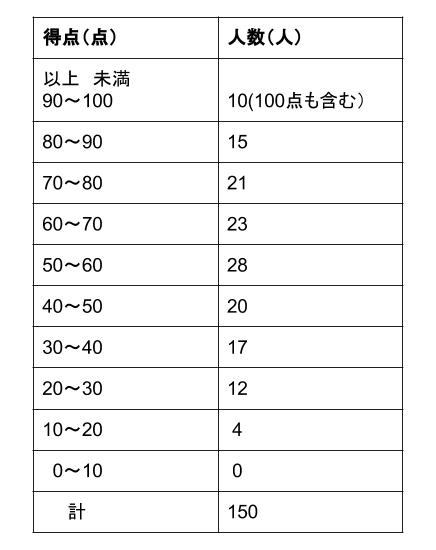
(考え方は同じです、 「値」の代わりに「階級値 「(概数)が近似値だ!」 ・ 「数学 研究機関」の 場面 では、「(概数)は近似値ではない!」 「(概数)が近似値だ!」 となるのかもしれませんね! 扱う場面で、「概数」にとどまったり、「近似値」になっ 以下のデータは,\ 生徒人の数学の試験結果である\ 階級幅を点とし,\ 階級値,\ 度 数,\ 相対度数の分布表を作成せよ\ さらにヒストグラムに表せ\ また,\ 40点以上の生徒 の割合は全体の何\%か 階級 データの値の範囲 階級値 各階級の中央の値よって、階級値を用います。 例1 表は、\(a\) さんの走り幅跳び \(\) 回の記録である。 中央値を求めなさい。 解説 \(\) 個の資料の中央値なので、 \(10\) 番目と \(11\) 番目の値の平均をとります。 \(10\) 番目の値は、\(440~450\) の階級の中にあるので、階級値 \(445\) です。 \(11\) 番目の値も、\(4

中1 数学 中1 87 代表値と散らばり Youtube
中1 数学階級値
中1 数学階級値-階級値についてです 0以上10未満の階級値 数学 中学生 3日前 マー坊 階級値についてです 0以上10未満の階級値は答えは5です でも0,1,2,3,4,5,6,7,8,9の真ん中は45です なぜ45でなく5なのですか 1 回答 くん 3日前 0〜10という階級の階級値は0と10の半分、と考えます。求め方は、 010階級値 は各階級の幅 塾に通っているのに数学が苦手! 数学の勉強時間を減らしたい! 数学の勉強方法が分からない! その悩み、『覚え太郎』が解決します!!! 投稿ナビゲーション 度数分布表とは?階級の幅と階級値および累積度数とヒストグラム 有効数字とは?桁(けた)数と四捨



Www Pref Hiroshima Lg Jp Uploaded Attachment Pdf
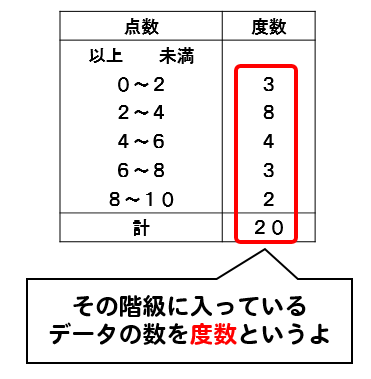
階級値とは 階級の中央の値をその階級の 階級値 といいます。 例えば 0点以上2点未満の階級の階級値は1点 10点以上13点未満の階級の階級値は115点 となります。 階級値の求め方 階級値は、小数になってしまうことも多く計算ミスが起こりやすい値の1つこの度数分布表では階級が \,5\, つあります。 \,10\, 点以上 \,15\, 点未満の階級 \,15\, 点以上 \,\, 点未満の階級 \,\, 点以上 \,25\, 点未満の階級階級値を英語に訳すと。英訳。〔数学で〕class value 80万項目以上収録、例文・コロケーションが豊富な無料英和和英辞典。
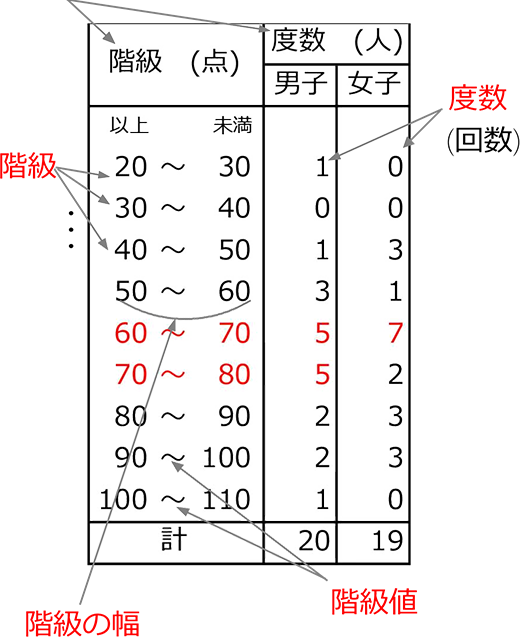
右の表は,クラスの全生徒25人分の数学の得点をまとめた度数分布表である。階級の幅は何点か。 解説 やり直す 19 点 点 21 点 100 点 階級値 例題2 階級(cm) 階級値 度数(人) 以上~未満 150~160 ア 2 160~170 イ 9 170~180 ウ 12 180~190 エ 4 合計 27 右の表は,クラスの各階級の最大値と最小値の差。 度数 各階級にはいる資料の個数(人数)のこと。 度数分布表 資料をいくつかの階級に分け、階級ごとに度数を示して分布の様子をわ かりやすくした表のこと。 階級値 度数分布表で、各階級の真ん中の値のこと。 ヒストグラムヒストグラムの中央値は「中央のデータが属する階級の階級値」 高校数学を解説するペンギン。 苦手な子でも分かる数学ブログを作成中。 勉強に本気な高校生のコミュニティを作りたい 21年完全版映像授業おすすめランキング!全10社を徹底比較! 21
中学数学 定期テスト これを階級値といいます。たとえば,13~14の階級値は135です。 度数折れ線のことを,度数分布多角形ともいいます。 ここで紹介している内容は17年3月時点の情報です。ご紹介している内容・名称等は変わることがあります。 ※ このq&aでは、 「進研ゼミ中学講座<<L47 代表値平均値・階級値 の解答消去 L48 近似値・有効数字 の問題に進む>> 練習問題1 下の表は、あるクラスの男子7人、女子8人の体重を記録したものです。例題(ケ―ス数が偶数のときの中央値) 次は,ある数学のテストを 10 人に対して行った結果である.このテストの中央値を 求めよ. 80, 52, 35, 23, 93, 71, 18, , 47, 64 (解答) はじめに点数が小さい順に次のようにデータを並べかえる. 18, 23, 35, 47, 52, 64, 71, 80, , 93 ケース数は 10 なの



度数分布表から相対度数を求める 苦手な数学を簡単に




資料のちらばりと代表値 度数分布表からの平均値の求め方 中学数学 定期テスト対策サイト
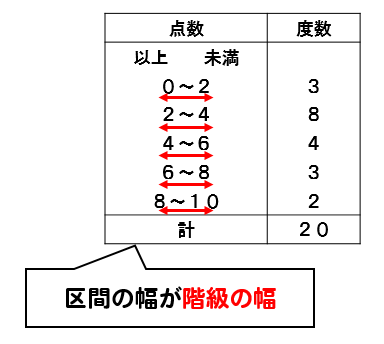
さらに、 各階級の端点の平均をその階級の階級値 数学 152 高校数学1から分かる順列と組み合わせの違い(公式&問題付き) 数学 三角関数のsin・cos・tanとは?図解ですぐわかる!超重要な公式と練習問題も 数学 1744 集合必ず覚えなくてはならない6つの記号と3つの平均値= 値の合計 資料の総数 度数分布表から平均を求める場合、各階級の資料の値はすべて階級値として計算する。 計算(1475×××××2)÷=1565 中央値を求めよ。 中央値とは資料を大きさの順に並べたときのちょうど真ん中の値数学a/データの分析 3 / 21 階級値と度数分布表 データを整理するために用いる区間を かいきゅう 階級といい, その区間の幅を かいきゅう 階級の幅という. とくに 階級の真ん中の値を かいきゅう 階級 ち 値という. それぞれの階級に入っているデータの値の個数をその階級の ど 度 すう 数と




度数分布 ヒストグラム 相対度数 平均値 代表値 無料で使える中学学習プリント



資料整理の用語 中学から数学だいすき
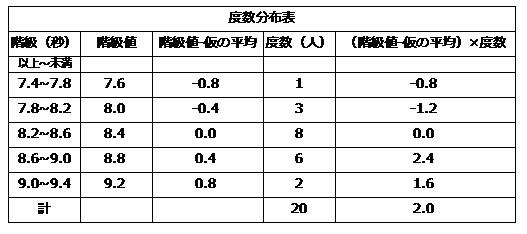
この分野が基礎になる科目は数学b 故にこのグラフを表計算ソフトで作成する場合は表2の2行の前の行に階級値が505であるもの、8行の後の行に階級値が745であるもの(それぞれ度数は0)を事前に挿入しておかなければならない。 平均値・分散・標準偏差 以下の表3は表2にいくつかの情報を平均値= {(階級値)×(度数)}の合計 度数の合計 階級値 階級の中央の値。35~40 kg の階級値は 37 5 kg。 ・仮の平均(平均に近いと考えられる値)を利用 する方法 はじめに,仮の平均を決めて, {(階級値-仮の平均)×(度数)}の合計 度数の合計階級値 度数分布表で,階級の中央の値のことを,その階級の階級値 という。 次は,階級値の例である。 • 階級「45kg 以上50kg 未満」の階級値 – 階級の幅を求めて,50 − 45 = 5(kg) – 階級の幅の半分を求めて,5 ÷ 2 = 25(kg) – 階級値は,4525 = 475(kg) – 次のように求めてもよい。



Www City Adachi Tokyo Jp Documents M 1 8 K Pdf




度数分布表から平均値を求める 中学1年の数学 身勝手な主張
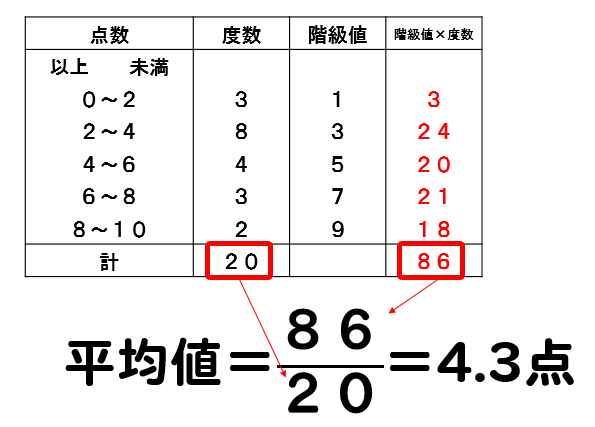
平均値 = (階級値 × 度数) 練習問題 各単元の要点 pcスマホ問題 数学 の例題 学習アプリ 中1 計算問題アプリ 正負の数 中1数学の正負の数の計算問題 加法減法乗法除法、累乗、四則計算 中学校数学学習サイト トップページ サイトマップ 更新履歴 サイトについて お問い合わせ 解説ヒストグラムの1つ1つの長方形の上の辺の中点(階級値)を、順に線で結んたグラフ のこと ただし両端は、度数0の階級があるものとしてつくる ・階級値階級の中央の値のこと 下の度数分布表は、ある中学校の生徒40人の体重について整理したものです。次の 1 問いに答えなさい。 階級(点扱う内容・用語としては,「平均値,中 央値,最頻値,階級 」が中1 から小6 へ,「多 数の観察や多数回の試行によって得られる 確率」が中2 から中1 へそれぞれ移行す るとともに,「累積度数」が中1,「四分位 範囲や箱ひげ図」が中2に加えられました。 また,中学校ではすべての学年で



中学数学 代表値 中央値 中学数学の無料オンライン学習サイトchu Su




相対度数の意味と計算方法 数学fun
度数分布表が与えられた場合,\ 階級内の値はすべて階級値であるとみなす 例えば,\ 150cm}以上160cm}未満の度数は2なので,\ 階級値155cm}が2人いるとみなす データの個数が{奇数個}であるからちょうど真ん中の値が存在する(1)階級1500円以上00円以下の相対度数7÷25=028答え 028(2)最頻値00~2500の階級値になる→2250答え 2250(3)平均値 平均値=仮平均+ズレ平均 を利用度数の最も大きい階級の階級値としての仮変数を 0 にすることの長所は,大きな度数でも 0 を掛けることになって,計算が省略できるからです.(上記の計算中の 0×7 ) 度数分布表の中央付近で,仮変数 0 にすると大きい方も小さい方も ±2 のように小さな整数値になって,計算が楽になるから



Studydoctor階級値と度数分布表での平均の求め方 中学1年数学 Studydoctor



練習問題 2 度数分布とヒストグラム 統計学の時間 統計web
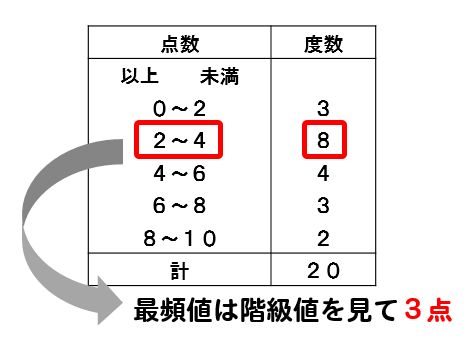
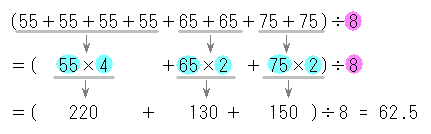
ここに数学のテスト結果が15人分あります。 テスト結果 63 91 46 53 7 37 97 15 44 66 74 59 53 62 (点) 上のようにデータを表すと全体の分布がいまいち分かりません。 それに対して、 テストの点数ごとに分けて表で表したものが度数分布表 です。 シータ 度数というのはその階級に当てはまる 階級値は以下の式で導けます。 $$階級値=\frac{階級の端階級の端}{2}$$ 例えば、0~69(kWh)なら $$階級値=\frac{690}{2}=345$$ 例えば、70~139(kWh)なら $$階級値=\frac{}{2}=1045$$ になります。 各級のど真ん中の数字を算出しているわけです。1、各階級の階級値を求める。 2、その各階級値に各度数をかける。 3、こうして算出された値を全て足し、度数の合計で割る。 これで平均値を求めることができます。 近似値・真の値・誤差の求め方 近似値・真の値は漫画で紹介しているとおり、円周率で



Www City Funabashi Lg Jp Gakkou 0002 Asahi J 0003 P D Fil 2nen0423 Pdf



代表値 平均値 中央値 最頻値 の意味と違い 数学fun
中央値の求め方(奇数) データの数が奇数個の場合には、ちょうど真ん中に位置する値を見つけることができます。 そのため、真ん中に位置する値が何番目になっているのかを求めることができれば、すぐに中央値が分かりますね! 中央値は何番目 階級値 の2乗と度数× このページは「高校数学Ⅰ:データの分析」の問題一覧ページとなります。解説の見たい単元名がわからな yorikuwacom 前へ 1 2 数学Ⅰ:データの分析 離散数学 Twitter Facebook LINE スポンサーリンク よりくわ先生 教科書より詳しい高校数学 分散と標準偏差数学17章データの分布「ヒストグラムや代表値の利用」<準備問題> 組 番 名前 次の ① ~ ④ にあてはまる語句を書きなさい。 (1)度数分布表において,各階級の度数の,全体に対する割合を,その階級の ① と いい,度数の合計が異なる資料も, ① で比較することができる。 (2) ① の



中1数学最頻値について このような度数分布表から最頻値を Yahoo 知恵袋



度数分布とは 表や多角形の作り方 平均値 中央値 最頻値の問題 受験辞典




中学数学 3分でわかる 階級値 ってなに Qikeru 学びを楽しくわかりやすく




中学数学 最頻値 モード の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



高校数学 度数分布表 階級値 相対度数 ヒストグラム 受験の月




代表値 平均値 中央値 最頻値 の意味と違い 数学fun




中1 数学 資料の整理5 最頻値と階級値 9分 Youtube



最頻値を求める 中学から数学だいすき




中1数学 平均値 と 中央値 練習編 映像授業のtry It トライイット



Q Tbn And9gct9g81v6fbuxe2zy40zobgjz7pv4jyf9dpik7xrlwfhfckmjg0k Usqp Cau




度数分布表から平均値を求める 中学1年の数学 身勝手な主張




数学における度数分布表とヒストグラムとは 中央値 最頻値も 高校生向け受験応援メディア 受験のミカタ




Descubre Como Resolverlo En Qanda



Www Chuo Tky Ed Jp Ginza Jh Resources Content 0513 Pdf



この画像の度数分布表から最頻値を教えてくださいm M度 Yahoo 知恵袋




階級値の求め方とは なぜ平均をとるのか わかりやすく解説します 遊ぶ数学




中1数学 最頻値 と 階級値 練習編 映像授業のtry It トライイット



数学の度数分布表がわかりません 階級値 度数 相対度数をどなたか教えて Yahoo 知恵袋




代表値 平均値 中央値 最頻値 の意味と違い 数学fun




中1 数学 中1 87 代表値と散らばり Youtube




中学数学 3分でわかる 階級値 ってなに Qikeru 学びを楽しくわかりやすく



中学数学 代表値 中央値 中学数学の無料オンライン学習サイトchu Su




最頻値とは 最頻値の意味と求め方を解説




中1数学 最頻値 と 階級値 例題編 映像授業のtry It トライイット




中1 数学 7 3 中央値 最頻値 Youtube




4 1 Descubre Como Resolverlo En Qanda




中学数学 3分でわかる 階級値 ってなに Qikeru 学びを楽しくわかりやすく



中学数学 資料の散らばりと代表値
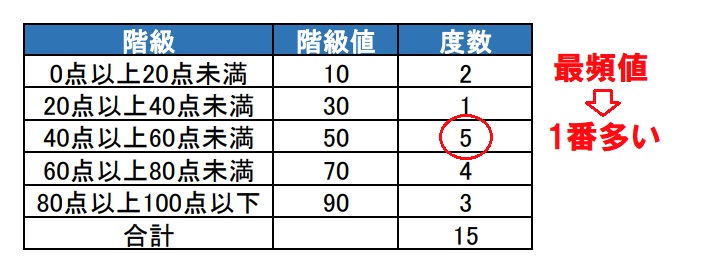



最頻値とは 最頻値の意味と求め方を解説



階級値とは何 Weblio辞書




中学数学 最頻値の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト



中学数学 度数分布表 ヒストグラム 中学数学の無料オンライン学習サイトchu Su




世界一わかりやすい数学問題集中1 7章 資料の活用



平均値 中央値 最頻値の違い 求め方 使い分け 計算問題 受験辞典




階級値ってなんですか あと求め方も教えていただきたいです Clear



1




中学数学 資料の散らばりと代表値



Math 平均値と仮の平均 働きアリ



中学数学 資料の散らばりと代表値



Www Pref Hiroshima Lg Jp Uploaded Attachment Pdf




中央値を含む階級が5冊以上10冊未満になる理由を教えてください Clear




中1数学 資料の散らばりと代表値 まとめ 中学生 数学のノート Clear



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ



無料 中1数学 基本問題 問題プリント 資料の活用2 近似値 145



1




中学1年生 数学 資料の整理 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
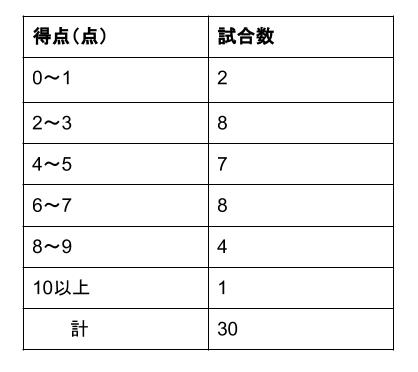



中学数学 代表値 最頻値 中学数学の無料オンライン学習サイトchu Su




平均値 中央値 最頻値の求め方といくつかの例 高校数学の美しい物語




中1数学 資料の整理のポイントと定期テスト予想問題 Pikuu



Math 平均値と仮の平均 働きアリ
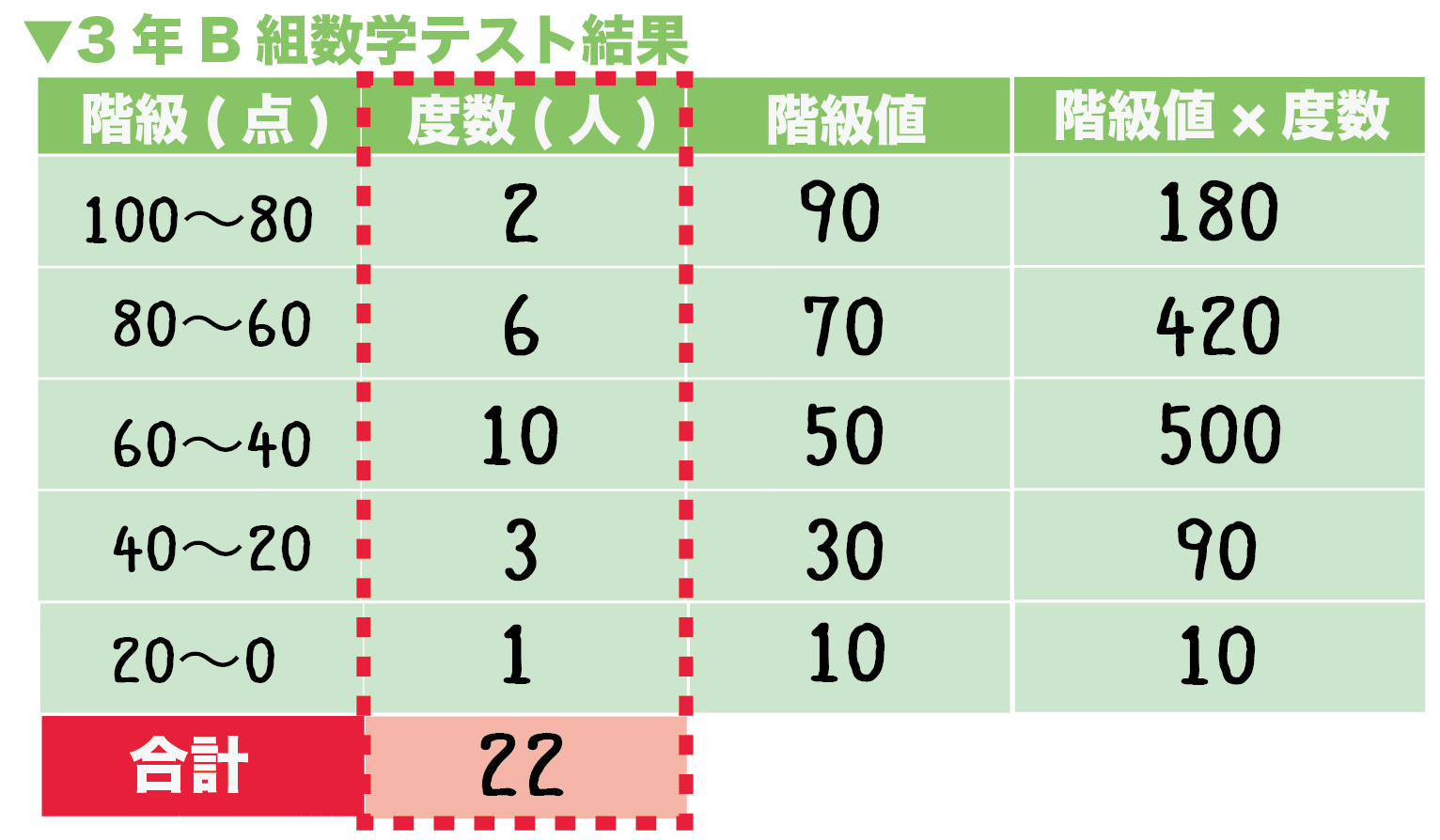



度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




中1数学 最頻値 と 階級値 練習編 映像授業のtry It トライイット



階級 階級の幅 階級値 度数 中学1年数学 資料の分析と活用




度数分布表とヒストグラム データの整理 の問題を解ける 数学ia Himokuri



無料 中1数学 基本問題 解答プリント 資料の活用2 近似値 145




最頻値 モード の求め方 高校数学 Youtube




ラノベでやり直し 中学数学3年間 猫村まきこ 資料の整理 小説投稿サイトノベルアップ



階級 階級の幅 階級値 度数 中学1年数学 資料の分析と活用




中学数学 最頻値 モード の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
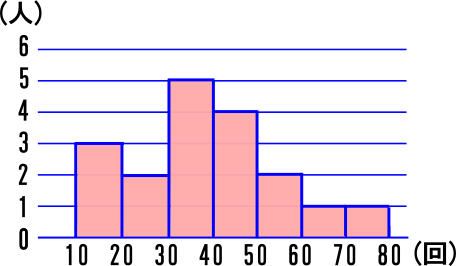



中学1年数学練習問題 代表値 平均値 階級値 中央値 最頻値の問題




中学数学 最頻値 モード の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




平均値 中央値 最頻値はどう使い分ける 3つの代表値を詳しく解説 遊ぶ数学



Http Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Yaruki Suugaku Documents M1018 Pdf



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




ねこ騙し数学




中学数学 3つの代表値の求め方 Qikeru 学びを楽しくわかりやすく




全く記憶にない 我が家の日常




資料の整理の問題の解き方 平均値と度数の合計から度数分布表の空欄の数字を求める 現役塾講師のわかりやすい中学数学の解き方



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




中1数学 資料の整理 度数分布表から最頻値を求める Youtube



無料 中1数学 基本解説 解答プリント 資料の活用2 近似値 145



資料のちらばりと代表値 度数分布表からの平均値の求め方 中学数学 定期テスト対策サイト




最頻値の求め方と中央値 平均値との違いと比較



数学の問題で 回答が無く困っています 表は ある店の1日の弁当 Yahoo 知恵袋




代表値 平均値 中央値 メジアン 最頻値 モード 最も使える中学数学範囲 教遊者




高校数学 代表値 中央値 メジアン と最頻値 モード 受験の月




数学の階級値がなぜ15分になるのかわかりません Clear




Descubre Como Resolverlo En Qanda




中1数学 最頻値 と 階級値 練習編 映像授業のtry It トライイット




中1数学 相対度数と代表値のポイント Examee



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




平均値と階級値について 苦手な数学を簡単に
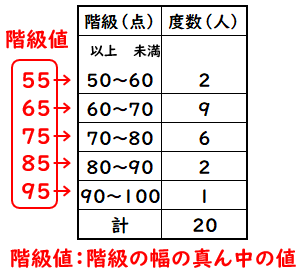



代表値 平均値 中央値 最頻値 の意味と違い 数学fun
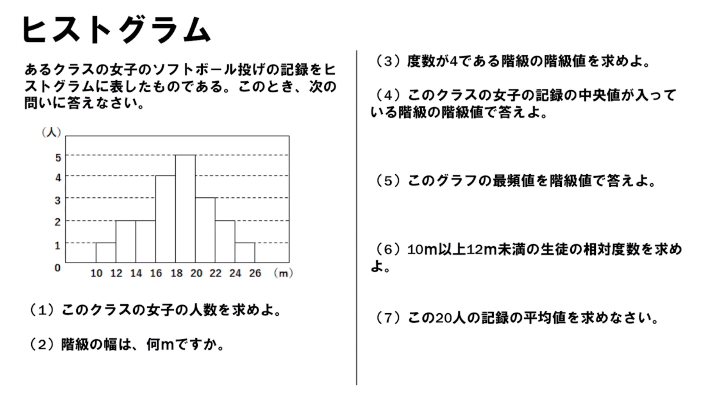



中1数学 資料の整理のポイントと定期テスト予想問題 Pikuu



練習問題 2 度数分布とヒストグラム 統計学の時間 統計web




度数分布表から平均値と最頻値を求める 苦手な数学を簡単に
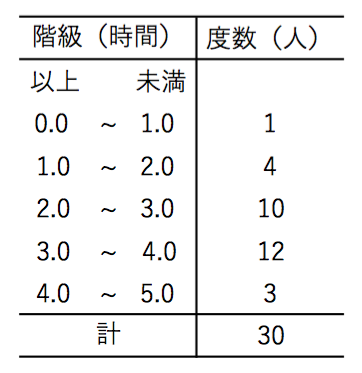



毎日問題を解こう 13 苦手な数学を簡単に




中1数学 最頻値 と 階級値 例題編 映像授業のtry It トライイット
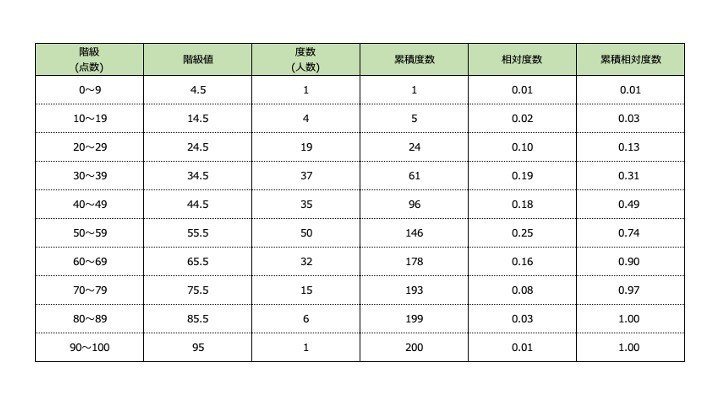



機械学習の統計学 度数分布表 ヒストグラムと平均値 中央値 最頻値について ししまる みらいのクルマをつくる人 Note




中学数学 3分でわかる 階級値 ってなに Qikeru 学びを楽しくわかりやすく



1
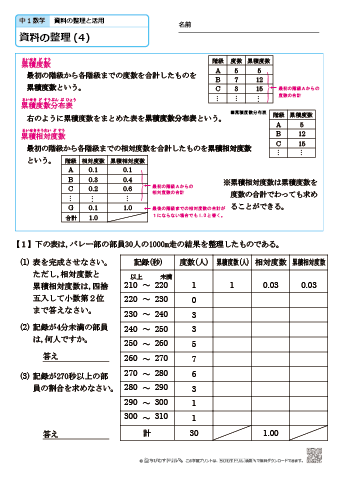



中学1年生 数学 資料の整理 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



0 件のコメント:
コメントを投稿