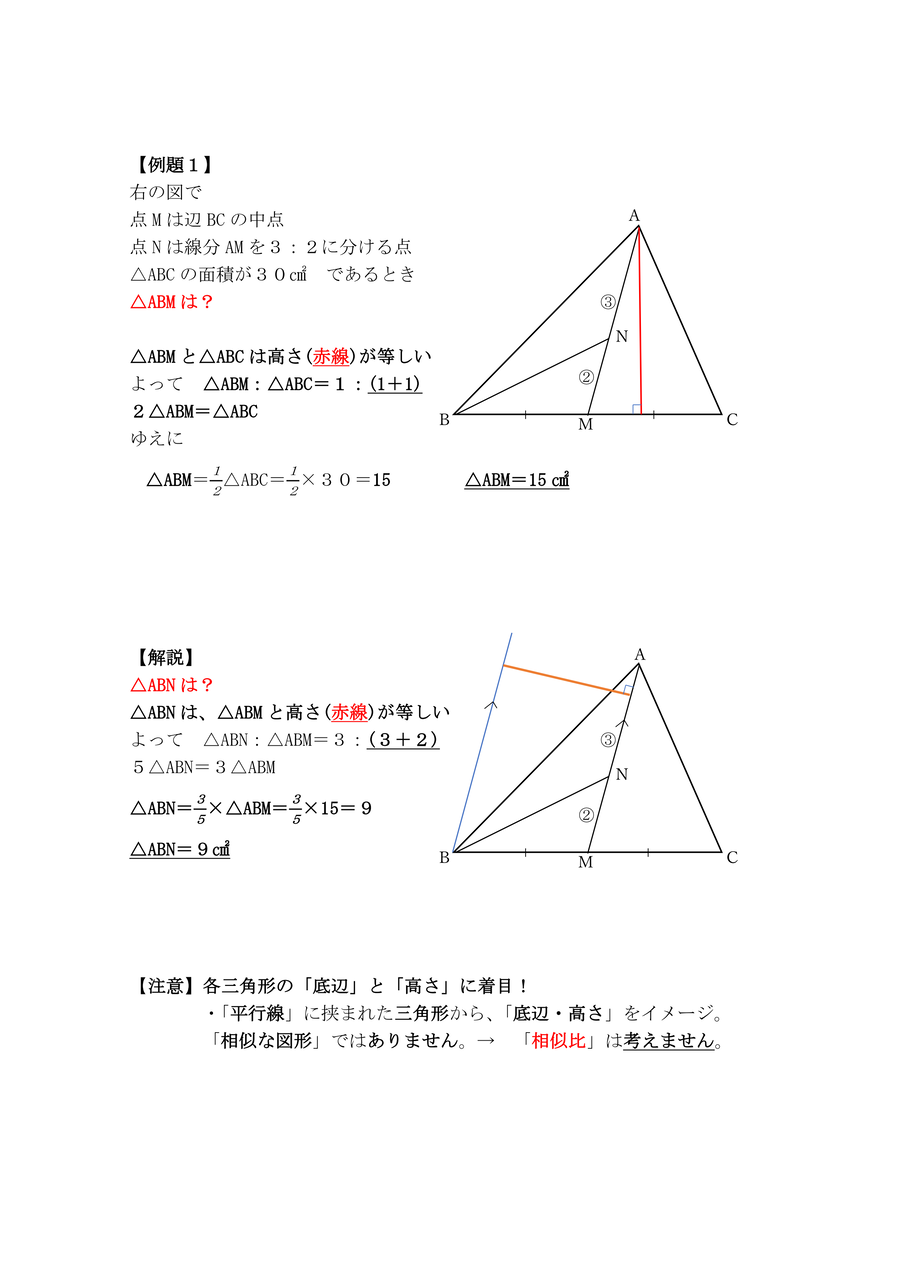
面積比の問題を考えていく上で とっても大切な面積比の知識を身につけておきましょう。 相似な図形において、面積比は相似比の2乗になる 比べる図形が相似であれば、相似比を2乗することで面積比を求めることができます。 つまり、台形の中から相似な図形を見つけていくことがポイントになってくるね。 相似な図形において、面積比は相似比の2乗になる 面積が360㎡ 面積の比を5:7にする 比が5;7ということは全部で12(5+7)で、キュウリの方は5/12と表すことができるので、 全体の面積×キュウリの比をすれば答えが出る。 360×5/12=150 150㎡ トマトの面積は 相似・線分比と面積比の徹底演習65問 中学受験算数の「相似・線分比と面積比」を完璧にするために、全65問の演習プリントを作成しました。 3レベルに分けてありますが、レベルAが必修問題、レベルBがR4や四谷でSS55程度の中堅校、レベルCが難関校レベルになります。 1 PDFファイル(問題・解答解説)
Studydoctor相似比と面積の計算 中学3年数学 Studydoctor
面積の比 問題
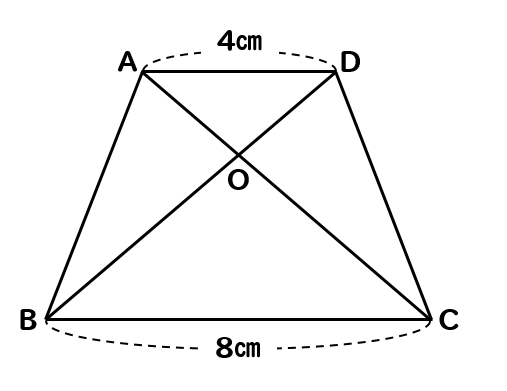
面積の比 問題-今年の1問 22年 算数星人/カワタケイタ 浦和明の星女子中−長方形の面積 22年;面積比1 右の図でbddcの比が45である。 abd adcの面積比を求めよ。 a b c d 右の abcdでeはabの中点eggdは14、 aegの面積が1cm 2 である。 a b c d e f g (1) agdの面積を求めよ。 (2) aeg ebdの面積比は何対何か。 (3) abdの面積を求めよ。 (4) abcdの面積を求めよ。 abcdの中に efghがある。斜線部分の面積を2等分する直線を描きなさい。



辺の比と面積比
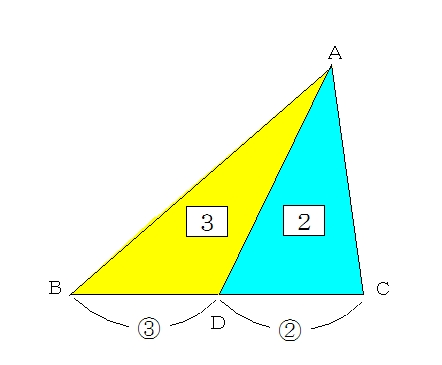
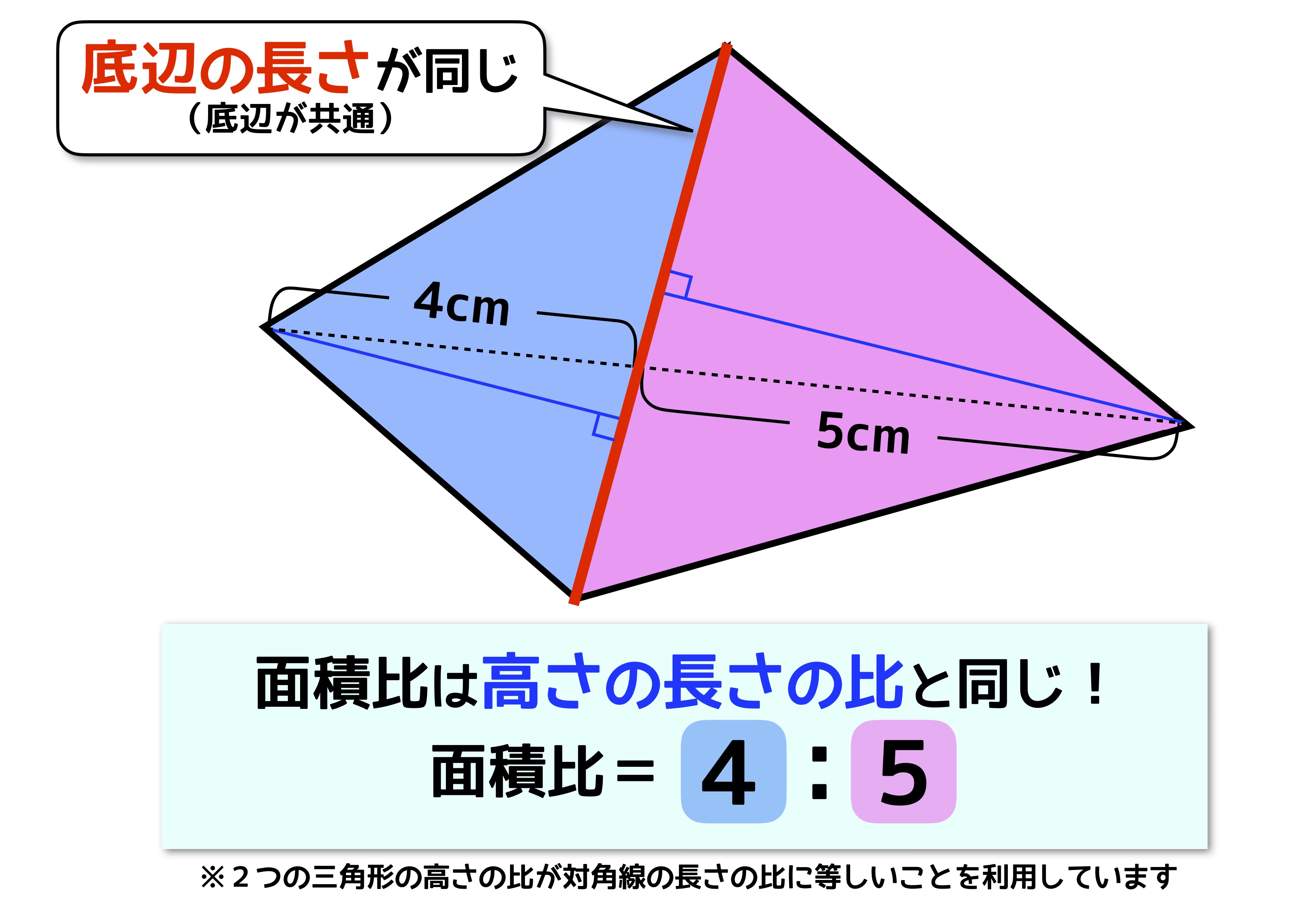
それでは、比を使った面積の問題を実際に解いていきましょう。 面積と辺の比とは 三角形の面積の公式が「底辺×高さ÷2」なので、「高さが等しければ、底辺の比と面積の比は同じになる」と考えられます。 この法則を使って面積を求めることができます。面積比の定番の問題 「砂時計型」「チョウチョ型」 図形の中でさらに図形に分かれてくると、面積比がわかりにくくなってしまう人もいます。 例えば、台形を対角線によって4つの三角形に分割したときの面積比を考える問題があります。これは、「砂時計型」や「チョウチョ型」と呼ばれる相似形を利用する問題で、受験生にとっては割と定番の問題なのですが ABEと AEDは高さがEF=EGで共通なので 、 底辺の比であるAB:ADが面積比となる 。 AB:AD=10:16=5:8 ABを5x、ADを8xとすると、 5x×8x=40x 2 =80 x>0より、x=√2 ABの長さは5√2cm。 (3)①
ベクトルから面積比を求める定番の問題です。 まずは始点が $P$ だとわかりづらいので、たとえば $A$ に変えるところから始めてみましょう。 解答Abcの面積が㎠のとき、 adeの面積を求めなさい。 d e b c 右の平行四辺形abcdにおいて、adをに分ける点をeとするとき、 次の問に答えなさい。 ① abeと defの面積比を答えなさい。 ② defの面積が㎠のとき、平行四辺形abcdの面積を 答えなさい。 2 32 8 3 no1 /2点 32 125 a b c d e f5年生 6年生 new 入試解説 埼玉 女子校 長方形 面積比 ★★★☆☆☆ (中学入試標準レベル) 印象に残った入試問題の良問を「今年の1問」と題して取り上げています。
面積比の問題と三角形、四角形の関係 「相似ではない」2つの四角形があります。面積比を求めてください。 高さがhで共通しています。よって面積の値は Aの面積 a×h=ah Bの面積 b×h=bh です。面積比=ahbh=abです。つまり高さの等しい四角形の面積比は「底辺の比率」と等しくなります。これは三角形でも同様です。 三角形の面積比の練習問題 問題 それでは、実際に問題を解いていきましょう! 問題1 次の図のように、点Aから引いた線と辺BCの交点をDとする。 以下の条件が成り立つとき、(1)〜(3)について ABDと ADCの面積比を各々求めなさい。 (1)BD:DC=3:1の場合 (2)BD=4, DC=2の場合 (3)BC:DC=6:1の場合 解答 《問題1の解説》 ABDと ADCは高さが同じなので、本日のお題 ABC において a = 7 , b = 5 , c = 8 のとき, ABC の面積を求めましょう 今日のお題は三角形の面積です 高等学校の数学まででは,重要なテーマですよね 高等学校の数学では,三角比とベクトルの単元でよく取り扱われて,大学入試の問題などに
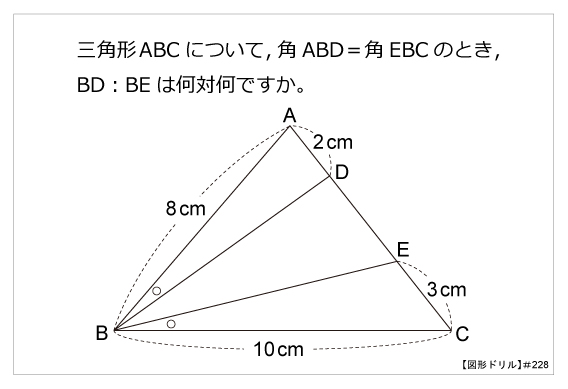



第228問 等しい角度と辺の比 図形ドリル 第228問 等しい角度と辺の比 算数星人のweb問題集 中学受験算数の問題に挑戦




三角形の面積比 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください
面積比の基本的な問題です。応用問題に入る前に、このレベルの問題を確実に出来るようにしておきましょう。 ポイント 高さの等しい三角形は、底辺の比が面積比になる→図の中で高さの等しい三角形をすぐに見つける練習をしましょう。 台形、平行四辺形は三角形2つ分→面積比は 三角形の底辺 台形の上底+下底 3つ以上に分かれた三角形の中の面積比は面積比 次の問いに答えよ。 BCCD=23のとき、面積比 ABC ACDを求めよ。 A B C D MはBCの中点である。 面積比 ABM ABCを求めよ。 A B C M ADDB=AEEC=11, DFFC=EFFB=12である。 A B C D E F 面積比 DFE DFBを求めよ。 面積比 ADE DBEを求めよ。




平面図形をマスター 三角形の面積比 応用編その2
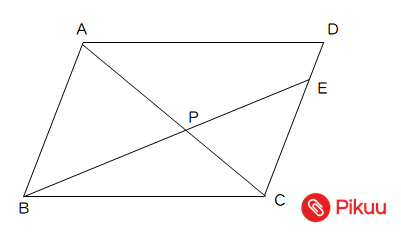



高校入試対策数学 面積比に関する対策問題 Pikuu
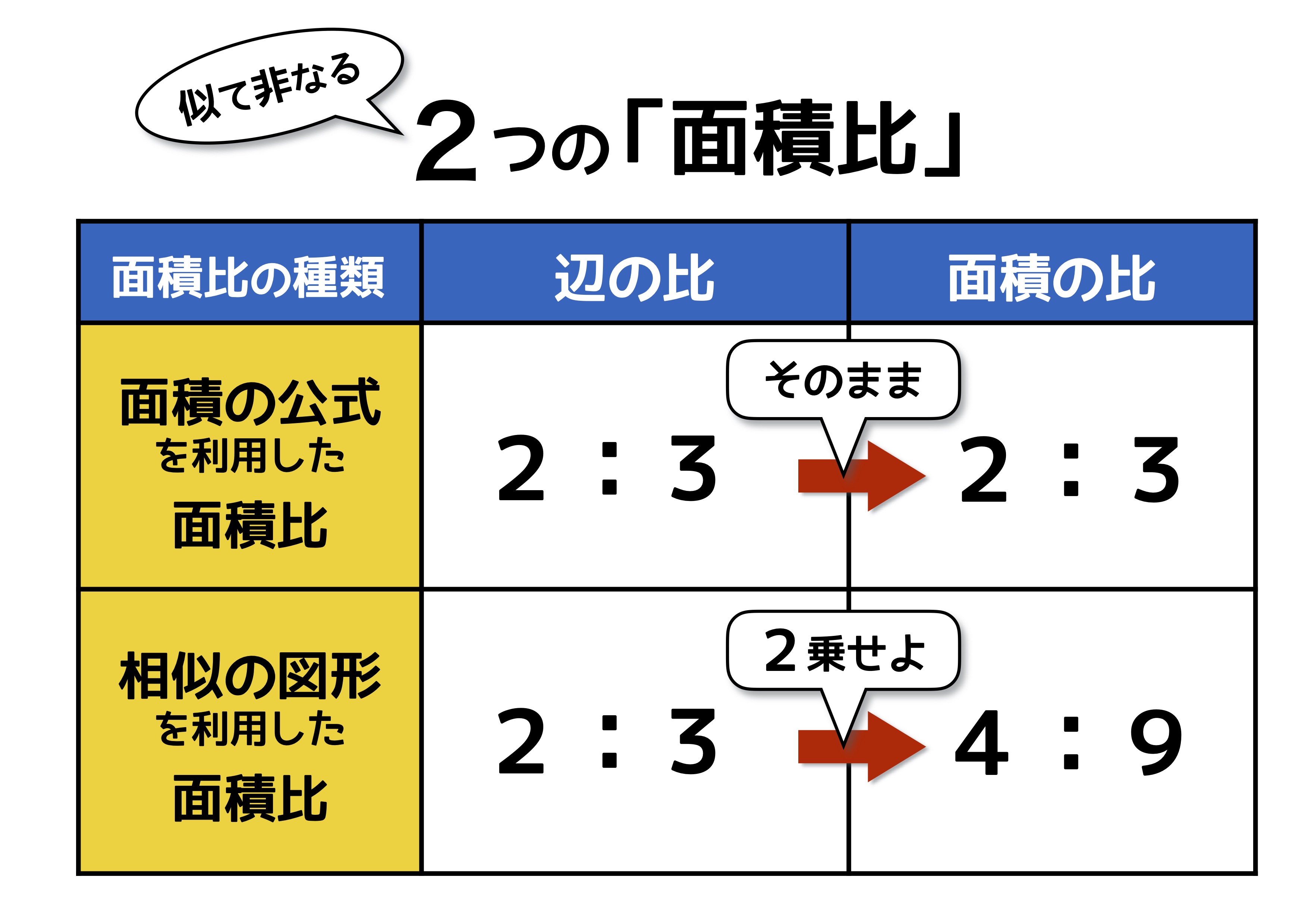



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo



Studydoctor相似比と面積の計算 中学3年数学 Studydoctor




中学受験算数 面積比の達人 仮 Yell Books みかん 本 通販 Amazon



相似比とは 1分でわかる意味 面積比 四角形と三角形の問題



面積と辺の比の関係を解説 図形の面積と辺の比の関係はテントやドリルで面積を求める



三角形の辺と面積の比 父ちゃんが教えたるっ
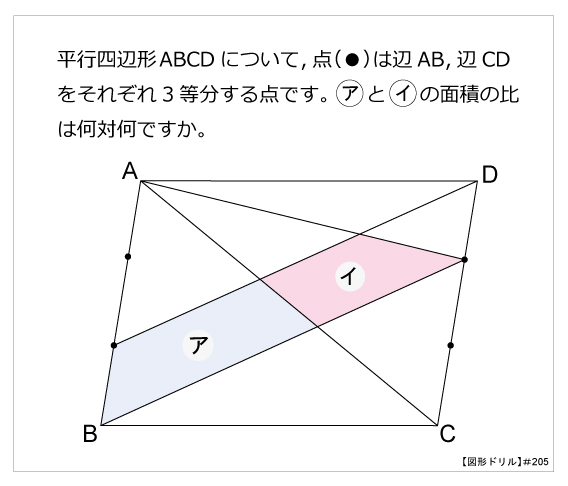



第5問 平行四辺形内の面積比 図形ドリル 第5問 平行四辺形内の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦
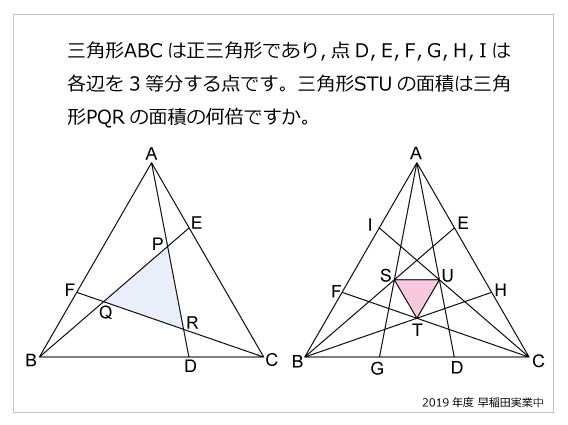



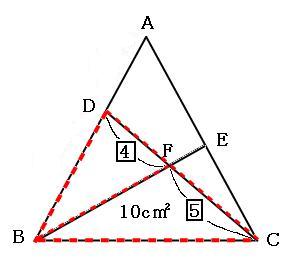
早稲田実業中 正三角形の面積比19年早稲田実業中 正三角形の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦
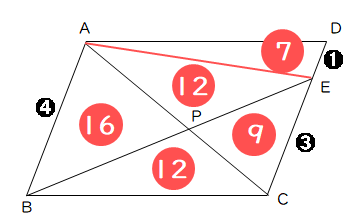



高校入試対策数学 面積比に関する対策問題 Pikuu



相似な図形 面積の比 苦手な数学を簡単に




数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo



面積比問題より 相似比の間違い これが中学入試に出た図形問題
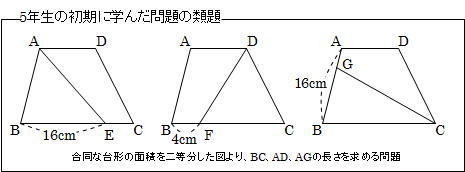



小5の学習ポイント4 辺の比と面積比 前田昌宏の中学受験が楽しくなる算数塾
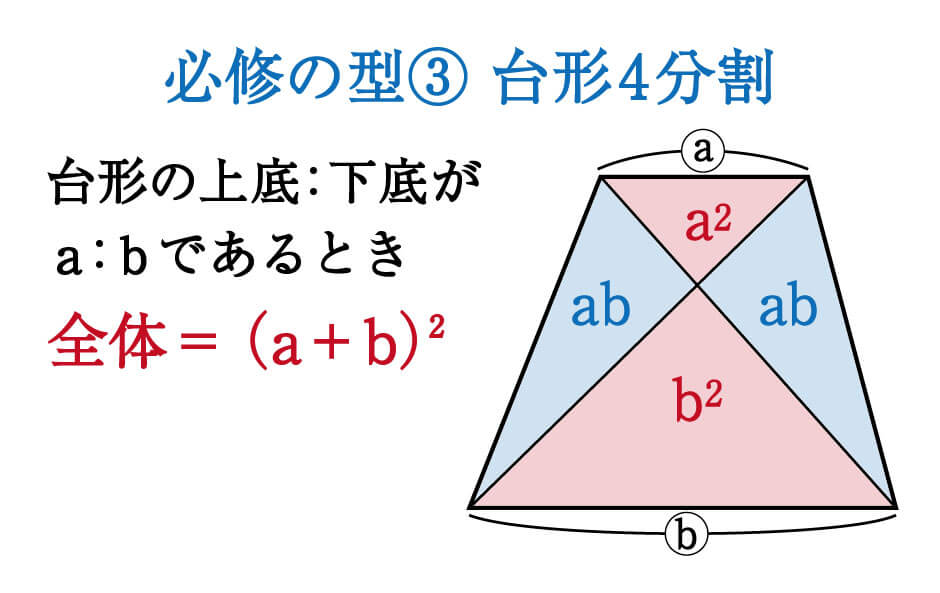



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



中3数学 相似比と面積比 の問題 どこよりも簡単な解き方 求め方 かずのかずブログ



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



相似 台形と面積比の問題を徹底解説 数スタ




平面図形をマスター 三角形の面積比 応用編その3




辺の比と面積比



攻略法 平行四辺形と面積 数樂管理人のブログ
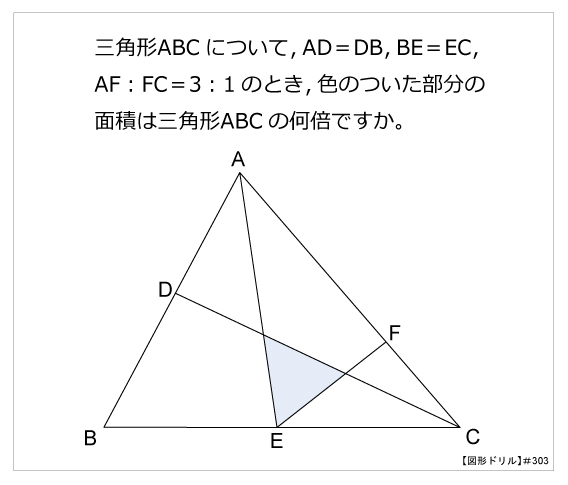



第303問 三角形の面積比 図形ドリル 第303問 三角形の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦




数学 中3 53 相似と面積 応用編 Youtube



中学校数学 証明のコツ 入試で差がつく 面積の比 体積の比 を得意にできる教材



ややこしや 線分の比 と 面積の比 名寄 算数数学教室より



中学3年数学練習問題 相似な平面図形の面積の比 図形と相似




三角形の面積比を解説 平面図形が苦手な人でもわかりやすい解き方 基本編 中学受験ナビ




平面図形をマスター 三角形の面積比 応用編その2



数学 なぜ面積比は苦手になりがちなの 面積比 集中特訓 1 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo
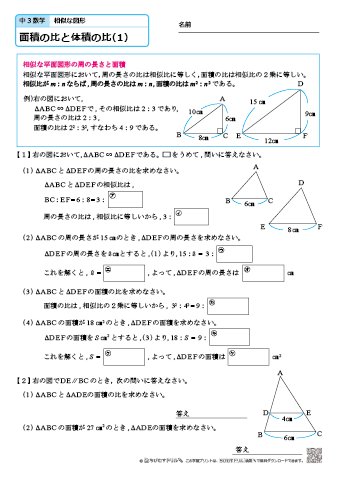



中学3年生 数学 面積の比と体積の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




図形の面積比 知っている人は5秒以内には解ける面積比の裏技 暇つぶしに動画で脳トレ
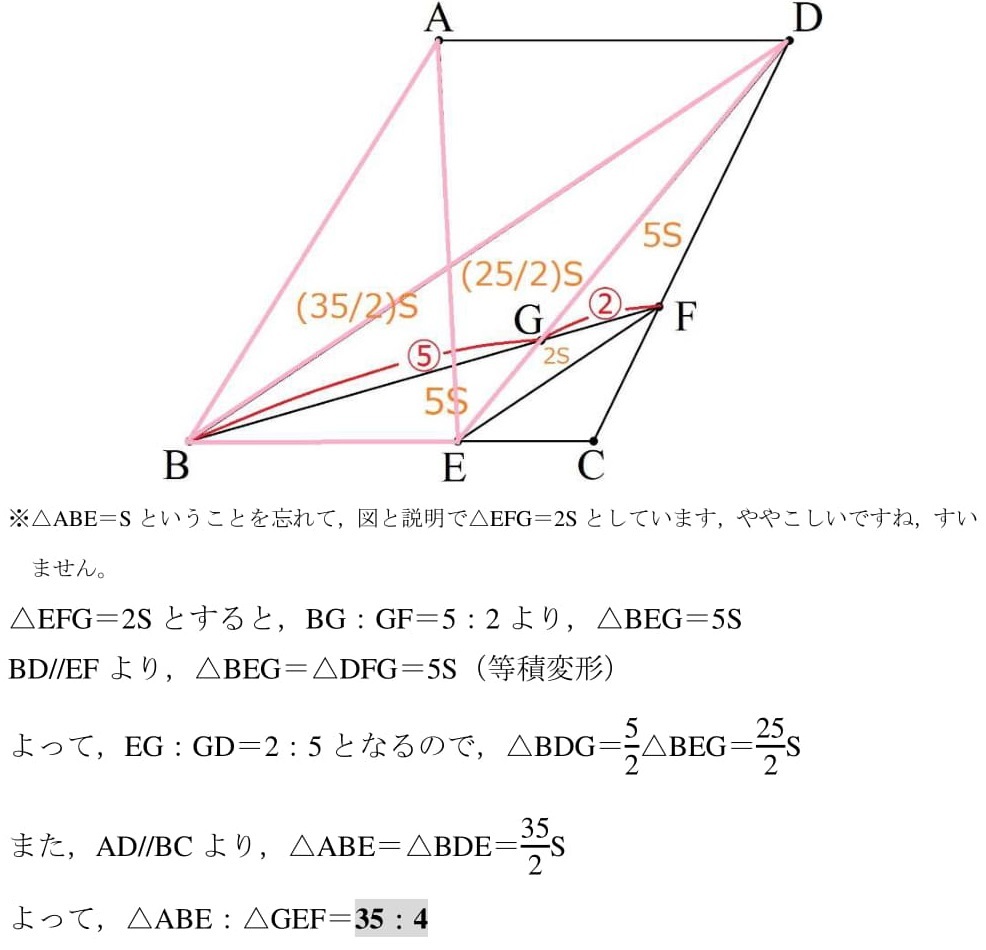



中2で解ける線分 面積比問題 21広島県大問3 高校入試 数学 良問 難問




平面図形をマスター 三角形の面積比 応用編その3



相似分野の応用問題 ラスボスっぽいの 多分それ連比です 面積の比 何倍 を求める問題も含めてかんたんな方法を解説します 教遊者
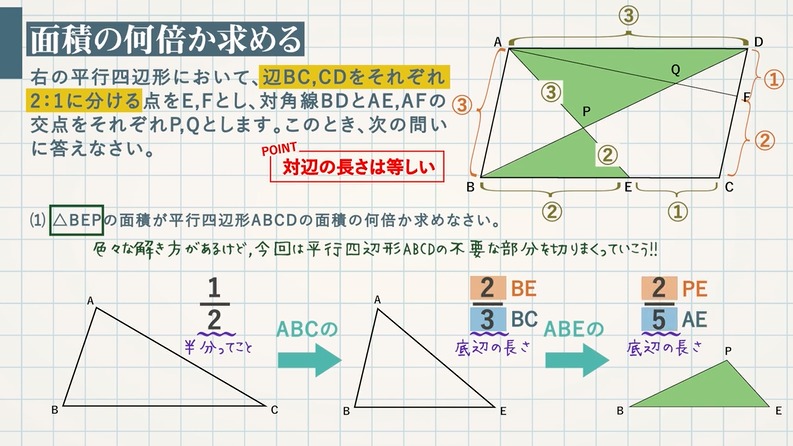



相似分野の応用問題 ラスボスっぽいの 多分それ連比です 面積の比 何倍 を求める問題も含めてかんたんな方法を解説します 教遊者




三角形の面積比 数学の偏差値を上げて合格を目指す



1




中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su
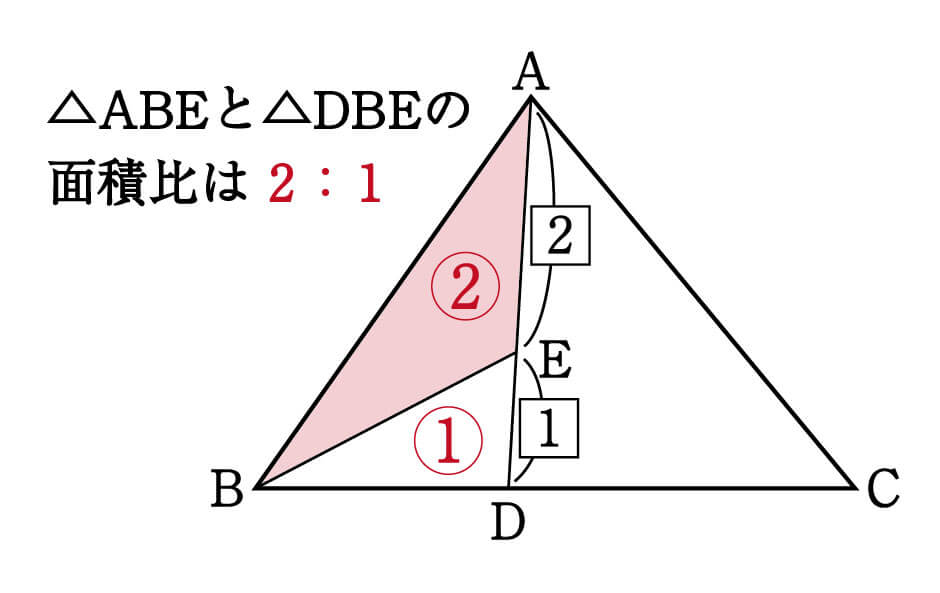



数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo
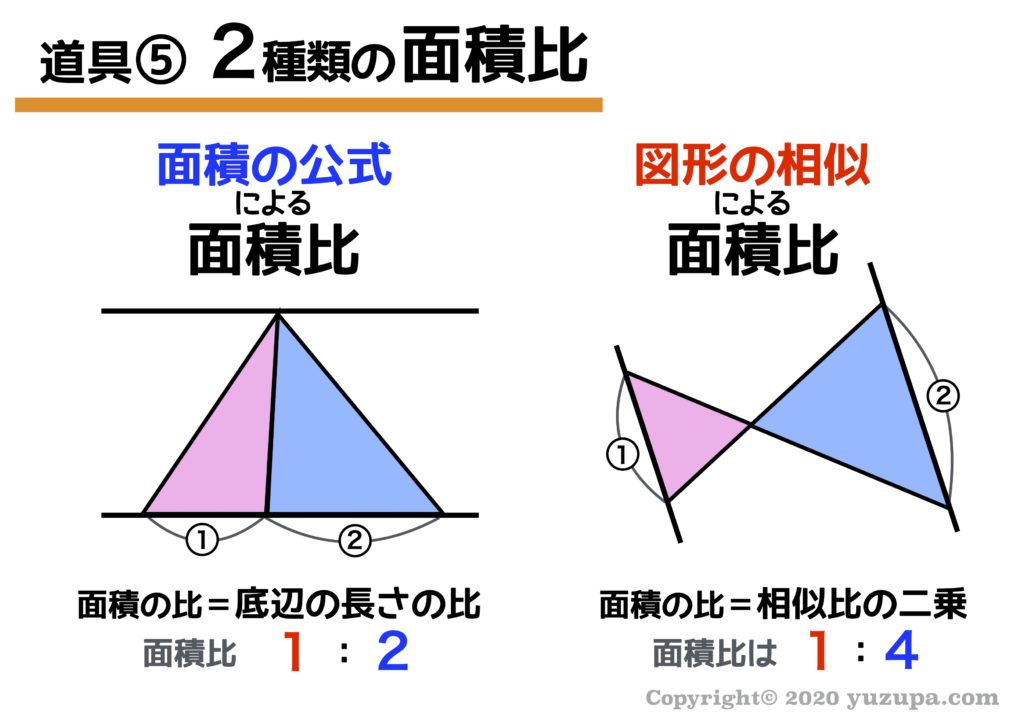



中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋



中学入試算数 よく出る問題はこれ 面積の比は 慶應義塾中等部 2012年 解けるかな 算数の難問に挑戦




小学6年生 算数 10月 辺の比と面積の比 速さ 1 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ




相似 平行四辺形と面積比の問題を徹底解説 数スタ



相似問題より 相似比と面積比の基本問題 これが中学入試に出た図形問題




中学受験算数 三角形の2辺の比と面積比の問題 Stupedia




相似比a Bのとき 面積比はa B になるのになんで ウ の問題は2乗をし Clearnote




相似 平行四辺形と面積比の問題を徹底解説 数スタ




相似な図形の面積比の問題 相似比を出してから二乗しよう 中学や高校の数学の計算問題




高校入試対策数学 面積比に関する対策問題 Pikuu




平面図形をマスター 三角形の面積比 応用編その2
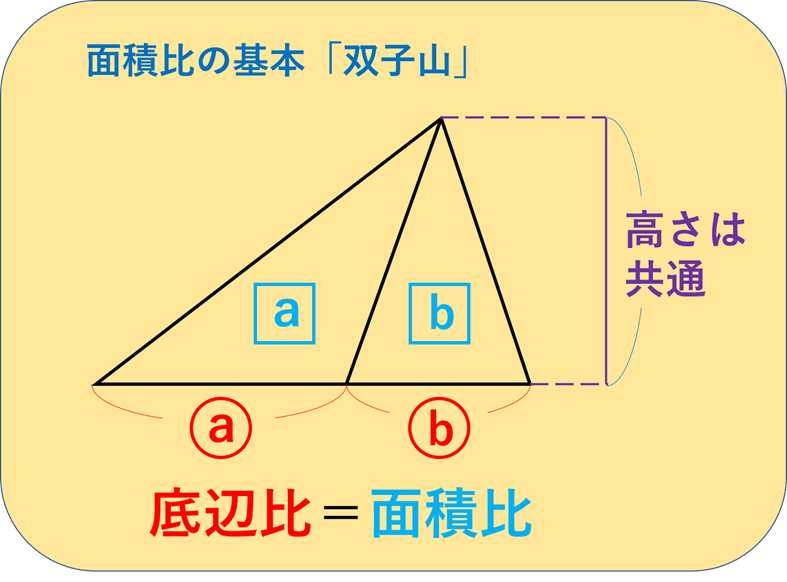



中学受験算数 平面図形 相似比と面積比の関係 中学受験プロ講師ブログ



相似分野の応用問題 ラスボスっぽいの 多分それ連比です 面積の比 何倍 を求める問題も含めてかんたんな方法を解説します 教遊者
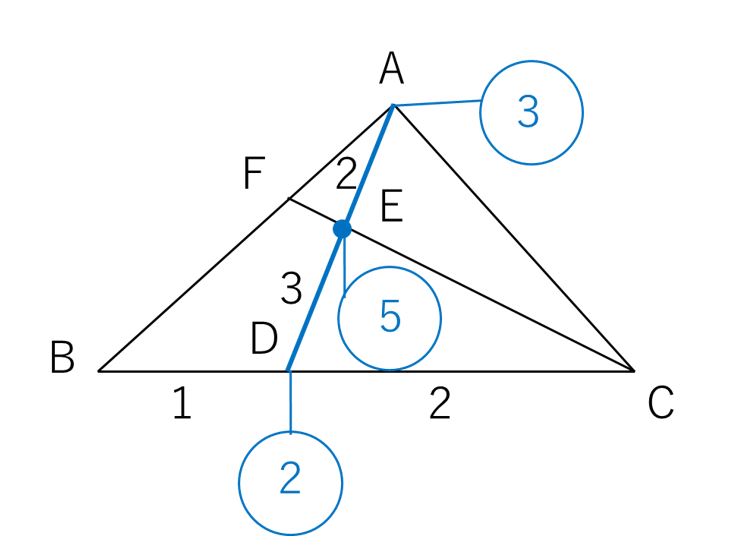



三角形の面積比をてんびんで解く 中学受験プロ講師ブログ



平行四辺形を分ける面積比の求め方 算数解法の極意




相似の面積比を求める問題 上級編 Youtube
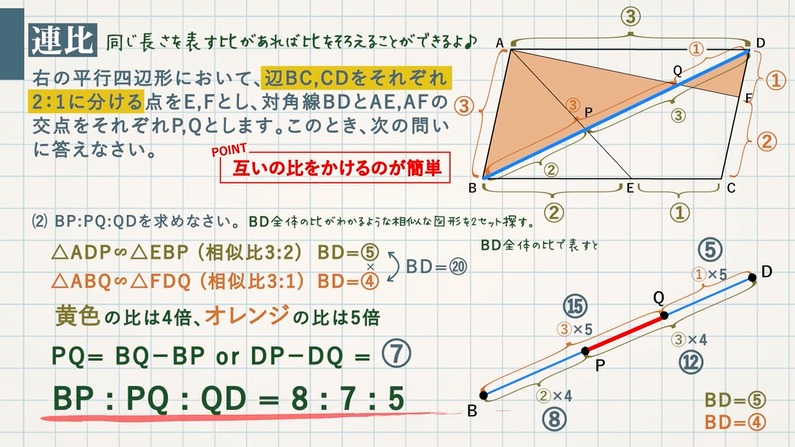



相似分野の応用問題 ラスボスっぽいの 多分それ連比です 面積の比 何倍 を求める問題も含めてかんたんな方法を解説します 教遊者



辺の比と面積比 等角三角形 富士山型 Next Stageのブログ



面積比 長さ比 これが中学入試に出た図形問題




メネラウス型 辺の比と面積比 Nextstage Warehouse



相似分野の応用問題 ラスボスっぽいの 多分それ連比です 面積の比 何倍 を求める問題も含めてかんたんな方法を解説します 教遊者
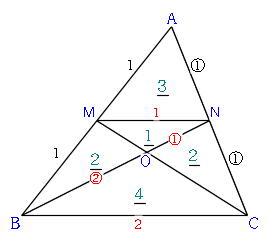



Mathematics 相似 4 面積と比 面積比は となりあった三角形で求める 働きアリ
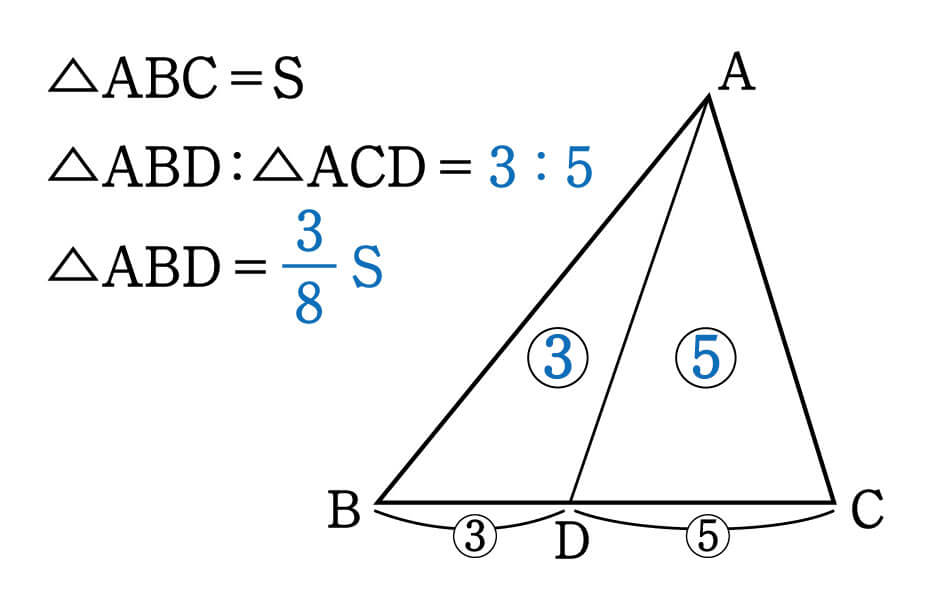



数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo
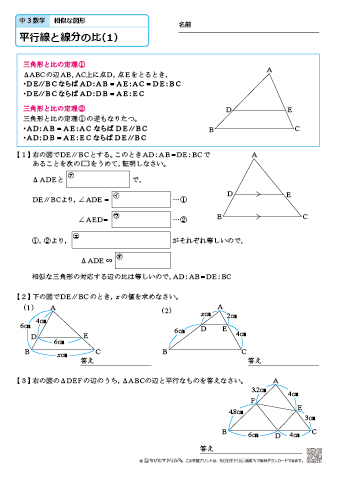



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



第5章 面積の比と体積の比 台形の相似比と面積比 中学生




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
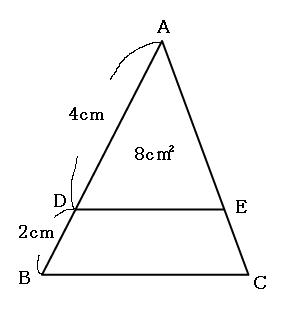



相似比と面積比と体積比の関係を解説 公式を使って面積や体積を求めよう




図形の面積比 知っている人は5秒以内には解ける面積比の裏技 Youtube




辺の比と面積比問題 考え方1 Youtube



1
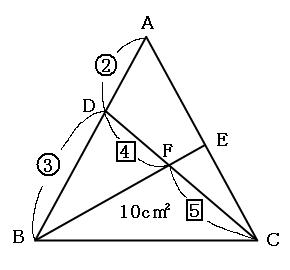



面積と辺の比の関係を解説 図形の面積と辺の比の関係はテントやドリルで面積を求める



数学i Aチェック リピート 第4章 2図形への応用 8 相似形の面積比 Pukiwiki
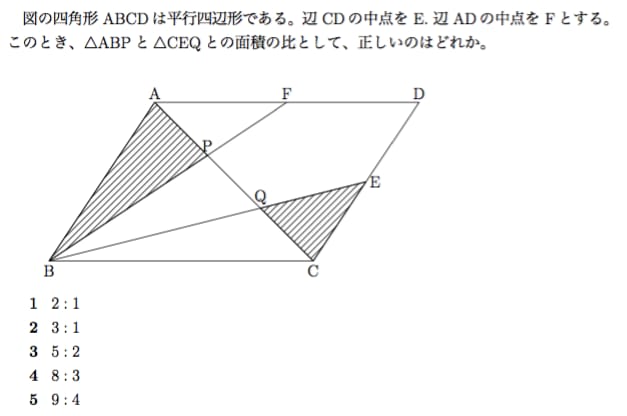



平行四辺形 中点 2つの三角形の面積比 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください
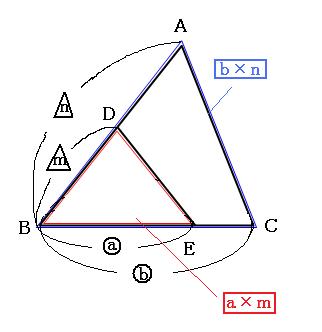



面積と辺の比の関係を解説 図形の面積と辺の比の関係はテントやドリルで面積を求める




平面図形をマスター 三角形の面積比 応用編その3
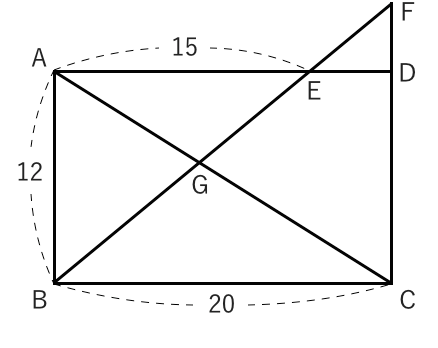



相似な図形 面積比の問題 苦手な数学を簡単に
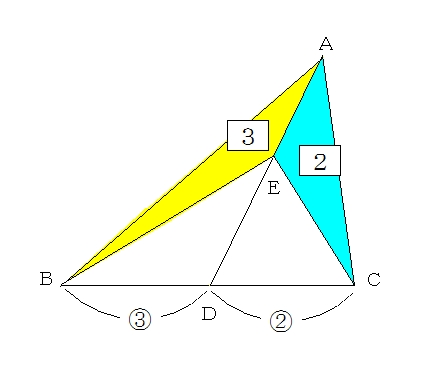



辺の比と面積比




辺の比 面積比 相似 16年東京都 高校入試 数学 良問 難問
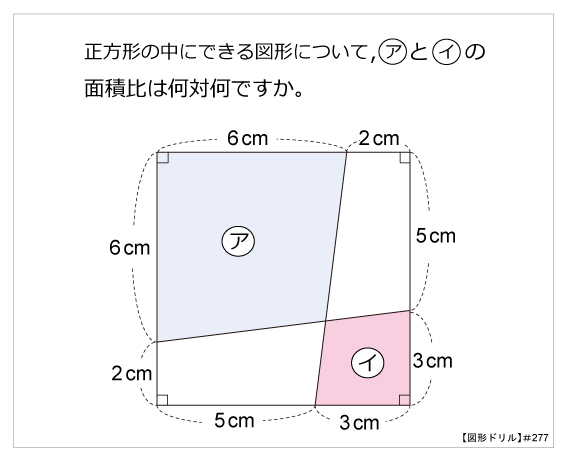



第277問 2つの四角形の面積比 図形ドリル 第277問 2つの四角形の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦



面積比の基本 中学受験準備のための学習ドリル
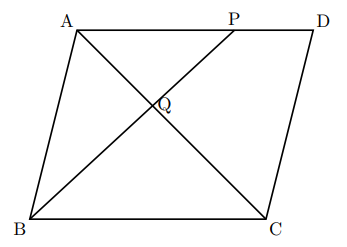



攻略法 平行四辺形と面積 数樂管理人のブログ
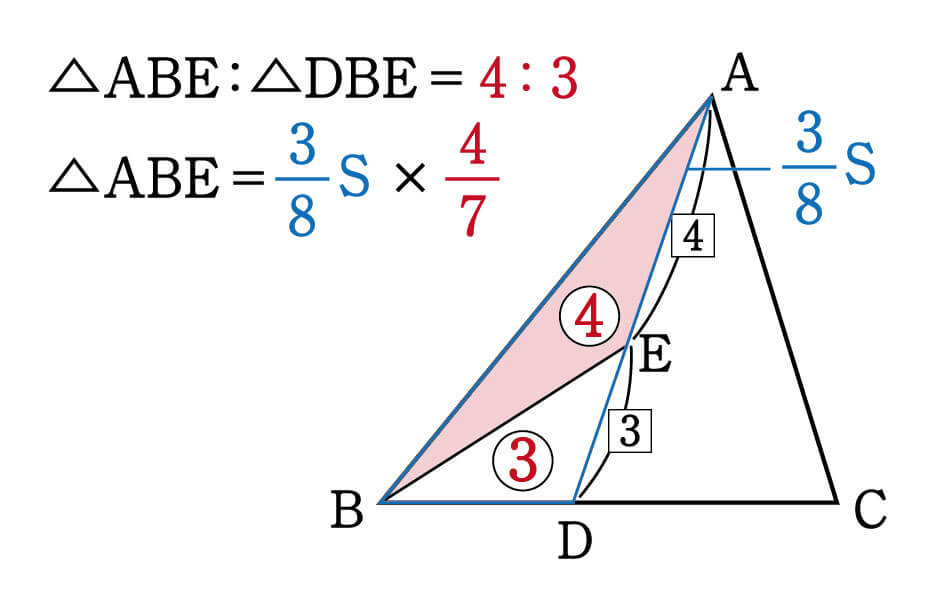



数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo



1
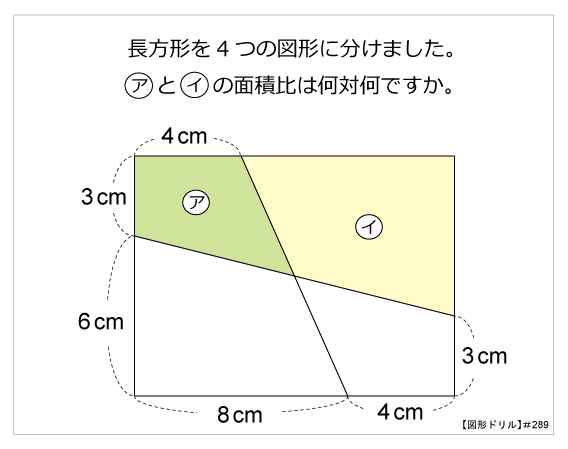



第2問 長方形と面積比 図形ドリル 第2問 長方形と面積比 算数星人のweb問題集 中学受験算数の問題に挑戦



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
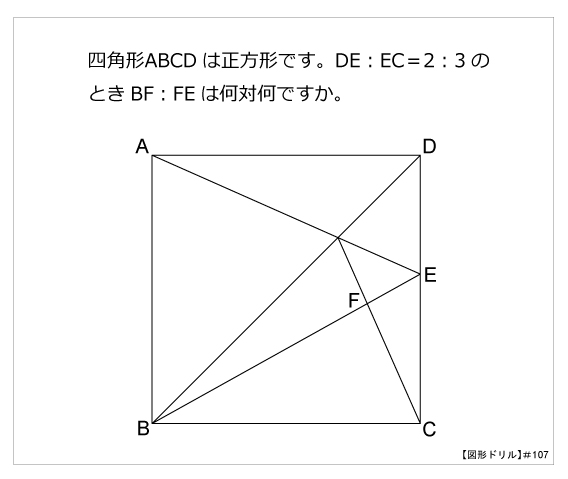



第107問 正方形と辺の比 図形ドリル 第107問 正方形と辺の比 算数星人のweb問題集 中学受験算数の問題に挑戦
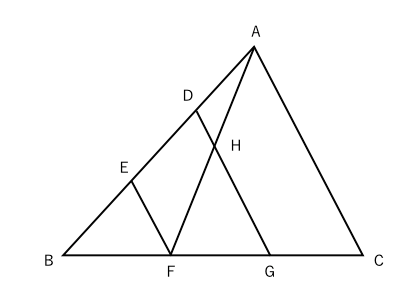



面積が何倍かを求める問題 応用編 苦手な数学を簡単に
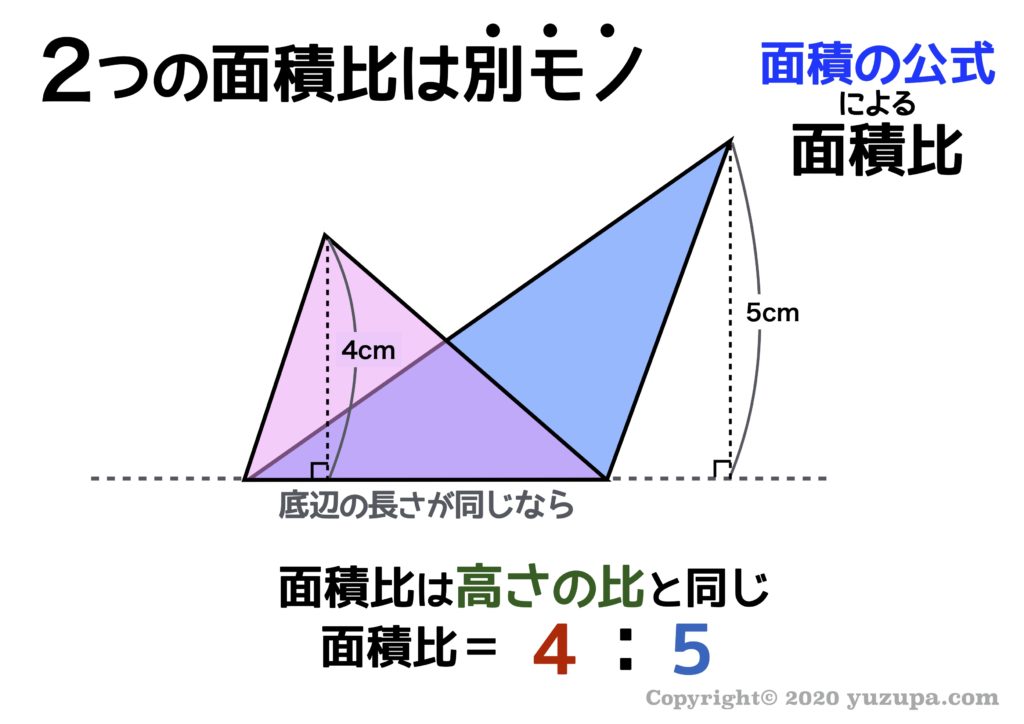



中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋



面積比 長さ比 中学受験ー算数解き方ポータル




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




中3 相似 相似分野の応用問題 連比 面積の比 何倍 かんたんな方法を解説します デジタル板書データ リクエスト動画 Youtube




中学数学 相似じゃない面積比 平面図形 Youtube
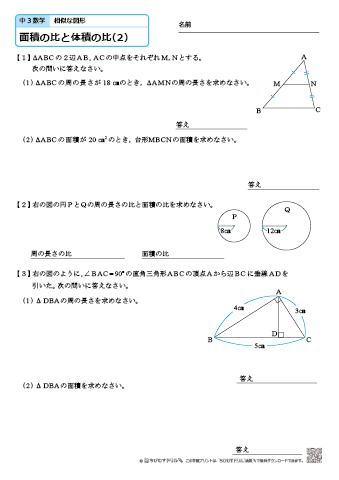



中学3年生 数学 面積の比と体積の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




算数図形編 面積比 線分比 相似 面積比を辺の長さで表そう 中学受験 高校受験パスナビ
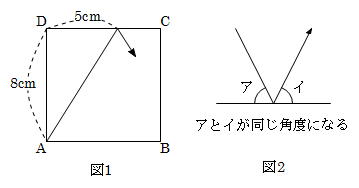



平面図形 辺の比と面積の比 前田昌宏の中学受験が楽しくなる算数塾



Homeroom 数学の入試問題を解くとき大切なこと 正しい入り口から入らないと問題は解けない 平面図形 相似 働きアリ
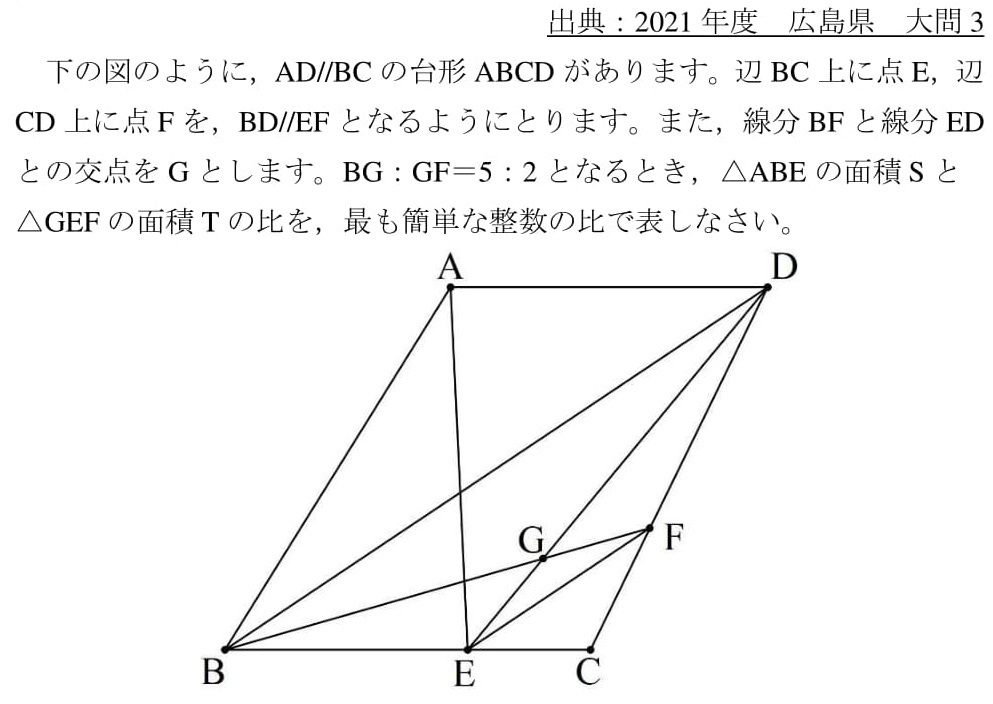



中2で解ける線分 面積比問題 21広島県大問3 高校入試 数学 良問 難問




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく



1



0 件のコメント:
コメントを投稿